密码学入门03 - 古典密码#3

前言

学习一下 Hill 密码。

0x01 数学基础

参考了数学乐。没有详细介绍矩阵的意义，但基本运算规则之类的讲得很清楚好懂。

1.1 矩阵

一个矩阵就是n行m列的数字表格，含义暂不考虑，只学习下矩阵的表示方法、运算规则，不然有点难读懂 Hill 密码的规则。

一个有 m 行，n 列的矩阵 A 的书写形式如下。 $$ A=\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix} $$

1.2 矩阵加法/减法

矩阵加减法规则如下。设有矩阵 A、B 如下。 $$ A=\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix},B=\begin{bmatrix} b_{11} & b_{12} & \dots & b_{1n} \\ b_{21} & b_{22} & \dots & b_{2n} \\ \vdots & \vdots & & \vdots \\ b_{m1} & b_{m2} & \dots & b_{mn} \end{bmatrix} $$ 则计算 A±B 的规则如下。 $$ A±B=\begin{bmatrix} a_{11}±b_{11} & a_{12}±b_{12} & \dots & a_{1n}±b_{1n} \\ a_{21}±b_{21} & a_{22}±b_{22} & \dots & a_{2n}±b_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1}±b_{m1} & a_{m2}±b_{m2} & \dots & a_{mn}±b_{mn} \end{bmatrix} $$ 性质：

只有行列数相同的矩阵，加减法才有意义
矩阵的加减法，就是矩阵中相同位置元素加减
矩阵加减法满足 交换律（A+B=B+A）和 结合律 （A+(B+C)=(A+B)+c）

1.2 矩阵数乘

数λ乘矩阵 A，即使将数λ乘矩阵A中的每一个元素，记为 λA 或 Aλ。

特别的，称 -A 为 A 的负矩阵。

性质：

满足 结合律 （(λμ)A=λ(μA); (λ+μ)A=λA+μA）和 分配律 （λ(A+B)=λA+λB）

1.3 矩阵乘法

先看矩阵的另一种表示形式：A=(a_ij)_mxs ，这种表示形式中，m 表示行数，s 表示列数，a_ij 姑且当占位，表示矩阵元素。

设 A=(a_ij)_mxs B=(b_ij)_sxn ，则 A=AB 是这样一个矩阵：

行数和左矩阵 A 相同，列数和右矩阵 B 相同，即 C=(c_ij)_mxn 。
C 的第 i 行第 j 列的元素 c_ij 由 A 的第 i 行元素和 B 的第 j 列元素对应相乘，再取乘积之和。

举例来说，将这两个矩阵相乘。

$$ A=\begin{bmatrix} 1 & 2 \\ 1 & -1 \end{bmatrix},B= \begin{bmatrix} 1 & 2 & -3 \\ -1 & 1 & 2 \end{bmatrix} $$ 结果是一个 2x3 的矩阵，每个元素计算如下： $$ AB=\begin{bmatrix} (1×1+2×-1) & (1×2+2×1) & (1×-3+2×2) \\ (1×1+-1×-1) & (1×2+-1×1) & (1×-3+-1×2) \end{bmatrix}= \begin{bmatrix} -1 & 4 & 1 \\ 2 & 1 & -5 \end{bmatrix} $$ 先用 A 的第1行，分别乘 B 的第1、2、3列，作为结果矩阵 C 的第1行。然后用 A 的第2行，分别乘 B 的第1、2、3列，作为结果矩阵 C 的第二行。

注意：相乘的矩阵应该满足条件，左侧矩阵列数等于右侧矩阵行数，计算才能进行。

性质（假设运算都是可行的）：

符合结合律 (AB)C=A(BC)
符合分配律 A(B±C)=AB±AC （左分配律）; (B±C)A=BA±CA （右分配律）
(λA)B=λ(AB)=A(λB)

1.4 矩阵转置

将 A 矩阵的行换成同序号的列所得到的新矩阵称为 A 的转置矩阵，记作 A' 或者 A^T 。 $$ A= \begin{bmatrix} 1 & 0 & 3 & -1 \\ 2 & 1 & 0 & 2 \end{bmatrix},A'=A^T= \begin{bmatrix} 1 & 2 \\ 0 & 1 \\ 3 & 0 \\ -1 & 2 \end{bmatrix} $$ 性质：

(A')'=A
(A+B)'=A'+B'
(AB)'=B'A'
(λA)'=λA'，λ是常数

1.5 对称矩阵

如果矩阵 A 满足 A'=A ，即 a_ij=a_ji ，则称 A 为 对称矩阵。

对称矩阵的特点是它的元素以主对角线为对称轴对应相等。

举例如下。 $$ A=\begin{bmatrix} 1 & 2 & 3 \\ 2 & 1 & 2 \\ 3 & 2 & 1 \end{bmatrix} $$

尝试将这个矩阵转置，令 a_ij=a_ji ，得到下面的矩阵，发现的确和原矩阵相同。 $$ A'=\begin{bmatrix} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{bmatrix}= \begin{bmatrix} 1 & 2 & 3 \\ 2 & 1 & 2 \\ 3 & 2 & 1 \end{bmatrix} $$

而原矩阵关于主对角线对称。

1.6 单位矩阵

单位矩阵是除了主对角线上是1，其他数字都是0的矩阵。任何矩阵和单位矩阵相乘都等于自身。

比如下面这个 3x3 矩阵。 $$ I=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

1.7 逆矩阵

如果有矩阵 B ，令 BA=AB=I，其中 I 为单位矩阵，则称 B 为 A 的逆矩阵，记为 A^-1 。对任意矩阵 A ，逆矩阵并不一定存在。

逆矩阵的作用是一定程度上代替了矩阵除法运算（矩阵不能做除法），例如已知矩阵A、B，求矩阵X，有下面的式子。

XA=B

如果有除法，那可以直接移项 X=B/A ，但矩阵只能相乘，所以我们可以在两边都乘上 A 的逆矩阵 A^-1 。

XAA^-1=BA^-1

因为 AA^-1 得单位矩阵 I ，所以左侧就变成了 XI。又因为任何矩阵和单位矩阵相乘都等于自身，所以 XI 可以简化为 X 。于是就得到了：

X=BA^-1

但是要注意次序！ AX=B 不能用上述方法做，因为矩阵乘法不一定满足结合律 （AB=BA），对于 AX=B 的情况，可以将 A^-1 放在式子之前，也就是 A^-1AX=A^-1B 。

1.8 行列式（拉普拉斯展开）

矩阵 A 的行列式记为 |A| ，和绝对值符号一样。只有方形矩阵才能计算行列式。方形矩阵就是行和列数目相等的矩阵。

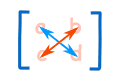
首先看 2x2 矩阵。 $$ A=\begin{bmatrix} a & b \\ c & d \end{bmatrix},|A|=ad-bc $$ 2x2矩阵的行列式就是简单的交叉相乘再相减。下图中蓝色是正，红色是负。

再看 3x3 矩阵的行列式写法，用矩阵第一行的元素，逐个去乘不在和这个元素同一行同一列元素的行列式，最后把这些值用加减号连起来。 $$ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix}= a \begin{vmatrix} e & f \\ h & i \end{vmatrix} -b \begin{vmatrix} d & f \\ g & i \end{vmatrix} +c \begin{vmatrix} d & e \\ g & h \end{vmatrix} =a(ei-fh)-b(di-fg)+c(dh-eg) $$ 更直观的图形化表示：

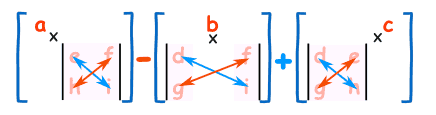
注意这个过程中的加减符号规律，a₁₁×(...) 是正，a₁₂×(...) 是负，a₁₃×(...) 又是正。

知晓这些规律后再看更大的矩阵，也可以依葫芦画瓢写出行列式。

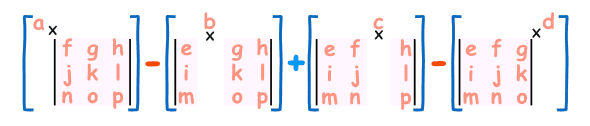
留意其中正负号出现的规律，+a₁₁ -a₁₂ +a₁₃ -a₁₄ 。

这种计算方法叫做 拉普拉斯展开 。

1.9 求逆矩阵的方法

2x2 矩阵的逆矩阵
初等行运算
余子式、代数余子式和伴随来求逆矩阵

2x2 矩阵的逆矩阵是： $$ A^{-1}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}^{-1}= \frac{1}{|A|} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix} $$

调换 a₁₁ 和 a₂₂
a₁₂ 和 a₂₁ 加上负号
除以原矩阵的行列式

3x3 或更大的矩阵的逆矩阵求法可以用初等行运算或用余子式、代数余子式和伴随来求逆矩阵。

0x02 Hill 密码

2.1 加密过程

首先给定一个密码矩阵 A。 $$ A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} $$

再给出明文：The quick brown fox jumps over the lazy dog

将明文转换成数字（ASCII），两个一组。比如 Th 就是 84 104 ，写成矩阵形式就是这样。

$$ P=\begin{bmatrix} 84 \\ 104 \end{bmatrix} $$

将密码矩阵 A 左乘明文矩阵 P ，C=AP，我们就得到了密文。

$$ C=AP=\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 84 \\ 104 \end{bmatrix}= \begin{bmatrix} 292 \\ 668 \end{bmatrix} $$

2.2 解密过程

解密过程就是利用密码矩阵的逆矩阵 A^-1 ，从密文求明文的过程，公式 A^-1C=A^-1AP 。

2x2 矩阵的逆矩阵求解方法看前面 1.9，求得逆矩阵如下。

$$ A^{-1}=\begin{bmatrix} -2 & 1 \\ 1.5 & -0.5 \end{bmatrix} $$

然后使用逆矩阵左乘密文：

$$ P=A^{-1}C=\begin{bmatrix} -2 & 1 \\ 1.5 & -0.5 \end{bmatrix} \begin{bmatrix} 292 \\ 668 \end{bmatrix}= \begin{bmatrix} 84 \\ 104 \end{bmatrix} $$

即可得到明文。

2.3 安全性

Hill密码的安全性体现在隐藏了单个字母的频率信息，加密矩阵越大效果越好。

Hill密码无法抵抗已知明文攻击，已知明文和密文时完全可以计算出加密矩阵。

总结

重点：

矩阵乘法、单位矩阵、行列式和逆矩阵

Hill密码是将明文转为矩阵后和加密矩阵相乘，加密矩阵即为加密密钥，加密矩阵越大效果越好。解密使用加密矩阵的逆矩阵作为密钥。

Hill 密码能隐藏字母频率信息，对抗仅密文分析，但无法对抗已知明文分析。