前言
B树和B树的变体(B+树)因为对磁盘IO/缓存友好的原因,常被用做数据库索引和文件系统的数据结构。
这篇博客主要是写一下B树如何插入和搜索,节点分裂机制以及如何自平衡。
节点结构
B树和一般的二叉搜索树在节点结构上有很大区别。B树是一种多路搜索树,B树的节点可以有多个后继节点,一个节点会保存多个键。单个节点最多保存M个键的B树称作M阶B树。
一个简单的 B 树节点结构如下。
class BTreeNode:
parent: 'BTreeNode'
entries: List[int]
children: List['BTreeNode']
B树要求除根节点外,每个节点最少包含M/2个元素,非叶子节点的 children 数量是 len(entries)+1。根节点不要求最少元素数量,其他约束不变。
插入节点
B树要求新的键只能在叶子节点上插入。如果叶子节点的键数量超过了上限M,则叶子节点执行 分裂 操作,将键分成三部分:中位数,小于中位数的部分,大于中位数的部分。
# 分裂前
[1,2,3,4,5]
# 分裂后
[1,2],3,[4,5]
中位数插入父节点,小于中位数的部分或大于中位数的部分创建新的子节点,插入父级节点。以插入元素 1-7 为例,图示如下。
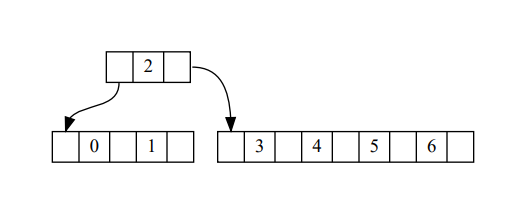
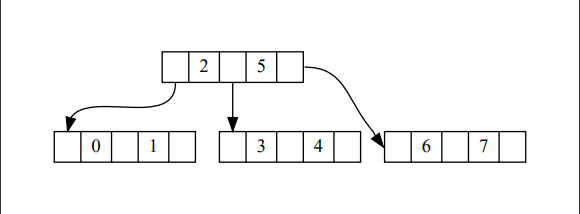
对于中位数在 entries 中间的情况不会更麻烦,只要记住新节点保存的都是大于中位数的部分,在entries插入键之后,找到对应的children下标插入即可。
def add_child(self, entry, child):
"""非叶子节点添加新元素
Args:
entry (int): 新元素
child (BTreeNode): 分裂出的新孩子
"""
# 遍历寻找比新 entry 更大的元素,如果不存在,则新 entry 添加到最后
for i, v in enumerate(self.entries):
if v > entry:
self.children.insert(i+1, child)
self.entries.insert(i, entry)
self.grow()
return
self.entries.append(entry)
self.children.append(child)
self.grow()
完整代码会在文末给出。
自平衡
B树是一种自平衡树,B树做到自平衡的方式比较特别。下面的内容都是我个人对B树的理解,偏见警告。
一般的二叉搜索树插入元素时,会把元素插入到叶子节点上,叶子节点就变成了中间节点,子树会随着插入的元素增长而变高,于是在子树之间出现不平衡。也就是说,一般的二叉搜索树生长方向是向下,往叶子方向扩展。
但B树正好相反:叶子节点不会变成中间节点,只会分裂兄弟节点,向父级节点插入键。而父级节点也会因为键超过M而分裂,一直到根节点。根节点分裂则会产生新的根,原来的根变成两个兄弟节点,树的高度随之上升。也就是说,B树的生长高度是向上的,插入操作对树高度的影响最终体现为根节点的分裂。
删除节点的规则也设计为保持这一特性,删除键对树高度的影响最终会体现为根节点和子节点合并,使得树高度降低。
搜索
B树的搜索和二叉搜索树差不多,不同的是节点会表示多个键,所以二叉搜索树中的比较操作会变成在多个键里查找值,并在中间节点没找到的时候递归搜索子节点。
def search(self, entry) -> bool:
for i, v in enumerate(self.entries):
if v == entry:
return True
# 如果没找到,而且当前元素比搜索值要大了
# 就从小于当前元素的子节点里递归搜索
if len(self.children) > 0 and v > entry:
return self.children[i].search(entry)
# 没有比搜索的键大的值,则从末尾的子节点(大于本节点全部键)递归搜索
if len(self.children) > 0:
return self.children[-1].search(entry)
return False
分裂和需要注意的问题
分裂节点写起来很简单,比 AVL 旋转要好懂很多。
def grow(self):
# 检查和处理分裂
# B-Tree 的增长方向是横向+纵向,横向是扩展兄弟节点,纵向是往根节点方向生长
if len(self.entries) > MAXIMUM_ENTRIES:
middle = self.entries[MIDDLE_ENTRY_IDX]
split_entries = self.entries[MIDDLE_ENTRY_IDX+1:]
split_children = self.children[MIDDLE_CHILD_IDX:]
self.entries = self.entries[:MIDDLE_ENTRY_IDX]
self.children = self.children[:MIDDLE_CHILD_IDX]
split_node = BTreeNode(self.parent)
split_node.entries = split_entries
split_node.children = split_children
for child in split_children:
child.parent = split_node
# 中间节点分裂的情况
if self.parent is not None:
self.parent.add_child(middle, split_node)
return
# 根节点分裂,生成新的根节点
self.parent = BTreeNode(None)
split_node.parent = self.parent
self.parent.children = [self, split_node]
self.parent.entries = [middle]
主要注意:
- 选择合适的中位数。如果
M是奇数,M+1除二没有余数,也选不出中位数。 - 新节点(
split_node和split_children)都需要重新调整parent属性,不要漏了。 - 中间节点的分裂要向上添加一个
entry和child,分别表示键和大于这个键的节点。- 这是个递归过程,上级节点也可能发生分裂,一直到根分裂。
- 这个过程会保留原节点(
self),可以理解为children的下标i表示children[i]这棵子树所有键小于entries[i]。children[-1]没有对应的entries下标,表示的是大于节点所有键的子树,相当于是二叉搜索树中的右子树。
- 根节点分裂会导致树的根发生改变,完成插入操作后需要重新确定根节点指针,不然会导致搜索出错或再次分裂的时候往错误的节点添加键,破坏搜索树的性质。
B树性能
B树的性能优势来自树的高度增长相对比较慢,选择合适的阶可以减少磁盘IO次数。另外就是一个节点包含多个键,提高键的储存密度,更符合局部性原理,相对于二叉搜索树来说对CPU缓存也更较友好。
对这个场景我能想到的几个关键因素主要有:
- 内存缓存。尽可能榨干可用的内存,避免频繁进行磁盘IO。
- 局部性原理。
其中局部性原理又分几项。
一个是内存的分页机制,在内存紧张的情况下如果节点集合大小不是一页的整数倍的话,会产生更多的缺页异常,造成更频繁地读盘(考虑使用了交换分区或 windows 页文件,又或者 mmap 等方式读取)。
另一个是CPU的高速缓存,如果结构填不满或者超出cache line 大小的话都会有影响。
当然,最后还是具体问题具体分析。给这篇博客找资料的时候看到的这篇文章很不错 gallery of processor cache effects,挺喜欢的。
总结
b树是多路搜索树。
b树插入节点总是在叶子,b树向根方向生长。
b树通过节点分裂和合并实现自平衡。
b树搜索和一般的二叉搜索树差别不大。
以及b树性能优势来自树更矮,节点更少,键更集中,符合局部性原理,减少磁盘io次数,合适的阶让结构对缓存更友好。