前言
还记得很久以前学数据结构只看到二叉树,讲到平衡,但平衡方法当时看纸质书手头也没有实验环境,后来就没继续学下去。现在有闲就重新捡起来学一下。先从AVL树继续看。
AVL树
AVL 树是以提出者名字命名的,Adelson-Velskii & Landis,俄国人,后来移居以色列。人怎么样不管啦。
AVL 树是一种平衡二叉树,左右子树高度差不超过1。保持平衡的方法是每次插入数据的时候发现子树不平衡,就把较高的子树提升为根,把根变成新的根的子树,把较高的子树变矮,较矮的子树变高,实现平衡。这个过程被叫做旋转,下面介绍旋转。
左旋转/右旋转
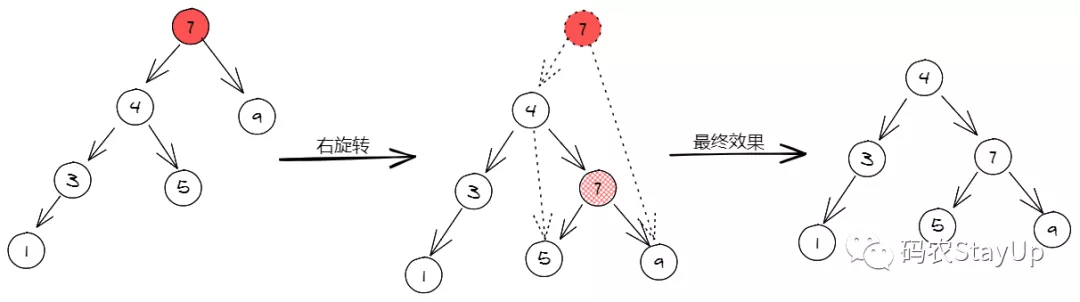
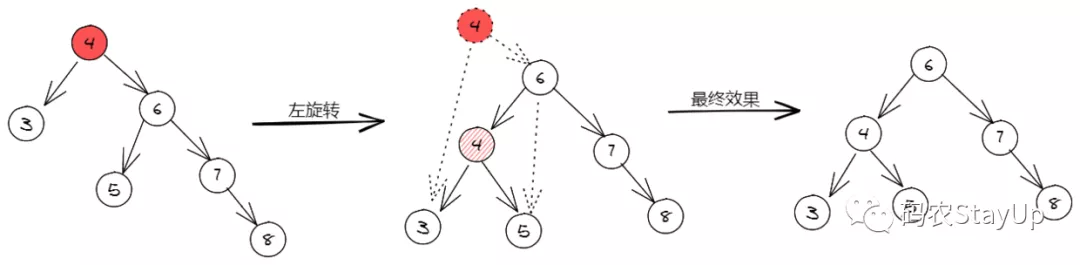
左旋转和右旋转的逻辑是一样的。如果右子树比左子树高,就把右子树提升成根。如果左子树比右子树高,就把左子树提升成根。提升右子树叫左旋转,提升左子树叫右旋转。
把子树提升成根会有点麻烦。比如右子树提升为根,原来的根和左子树怎么办?我们并不想重新平衡树的时候把整个左子树都删掉,那原来的根和左子树就必须插回新的树里。
我们知道右子树的 key 肯定比根和左子树所有节点大,所以根要插回树的话,一个很直接的想法就是把旧的根接到右子树左下角的叶子节点。
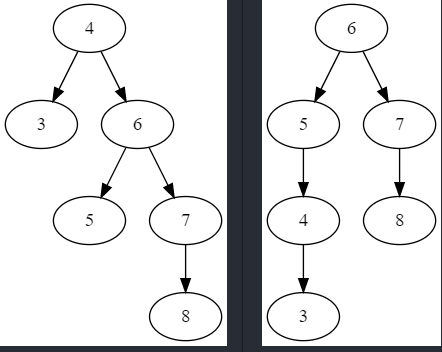
的确,这样保持了二叉搜索树的特征,但新的树依然不平衡:节点5的左子树高度2,右子树高度0,高度差超过了1。稍微想想就知道,旧的根和左子树直接接到左下角叶子节点的话,会让原本平衡的新树左子树高度增加,进而失去平衡。
解决方法也很简单,不要把旧的树接到新的树最小值上,而是把新树的左子树,移植成旧树的右子树,再把旧树移植成新树的左子树。这样一来,右子树的左子树和左子树的右子树不管怎么旋转,高度都一样。
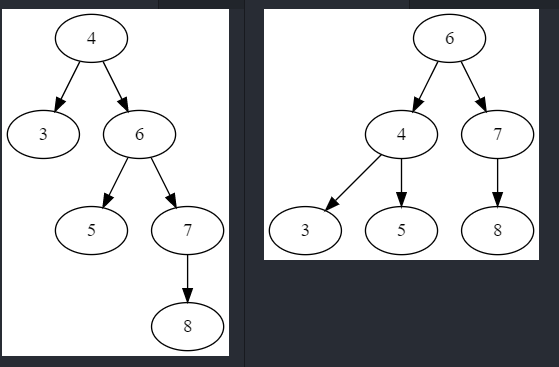
为什么这样可以保持平衡呢?首先AVL树的子树也是AVL树,所以子树的子树之间高度差也不超过1。左旋转、右旋转的的作用是让子树高度一侧升高,一侧降低——注意,左旋转只能降低右儿子的右子树高度,右儿子的左子树高度不变。右旋转只能降低左儿子的左子树高度,左儿子的右子树高度不变。
举例来说,上图中右儿子的右子树(4-6-7-8)较高,旋转后变成了(6-7-8),而原本的(4-6-5)变成了(6-4-5),高度不变。
这个规律很好理解,因为原来的右子树变成了根,整个右子树剩下的节点高度都降低了。而右子树的左子树变成了现在的左子树的右子树,和根的距离一样,所以高度不变。
左旋转让右子树的右子树高度-1,左子树的左子树高度+1。左子树的右子树高度等于右子树的左子树,旋转后新树的左右子树的高度相等。
双旋转
对于往左儿子的左子树插入节点造成的不平衡,右旋转可以实现降低左儿子的左子树高度,再次平衡。往右儿子的右子树插入节点造成的不平衡,左旋转可以降低右儿子的右子树高度,再次平衡。但对于左儿子的右子树或右儿子的左子树插入节点造成的不平衡,一次左、右旋转无法实现再平衡。
再看一个例子。
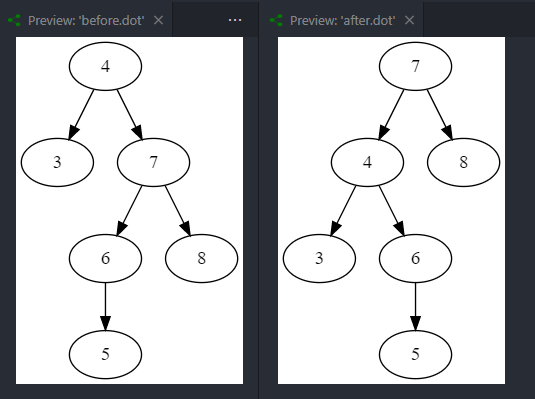
旋转前,右儿子的左子树(4-7-6-5)高度是4,旋转后(7-4-6-5)高度不变,依然是4,树仍然不平衡。解决办法也很简单,先把右子树(7)右旋,让右儿子的左子树高度低于右子树,再对整棵树左旋,也就是AVL树的双旋转。
一步一步看双旋转是怎么解决这个问题的。
第一步,右儿子的左子树比右儿子右子树高,所以将右儿子右旋,使得右儿子的右子树高于右儿子的左子树。
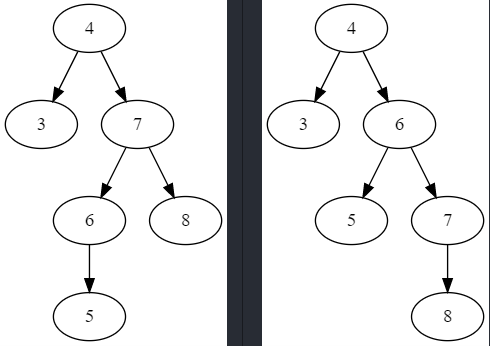
我们知道的左旋转时右儿子的左子树高度不变,右儿子的右子树高度-1。这一步前,直接对整棵树左旋时,最高的那颗子树(右儿子的左子树)高度没有变化,树依然不平衡,只是变成了右子树更矮,左子树更高而已。
而这一步之后,最高的子树变成了右子树的右子树。现在对整棵树左旋,右子树的右子树高度下降了,和原本右子树的左子树高度一致,达成平衡。
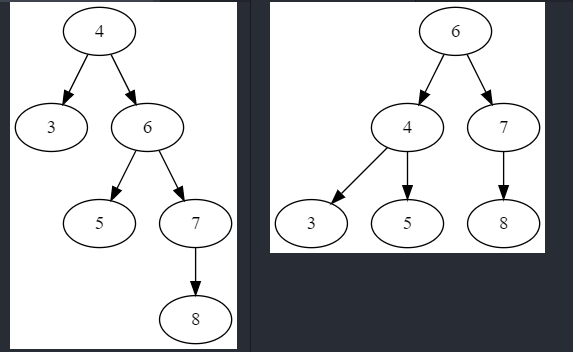
这个原则简单地说,就是左子树下最高的子树应该是左子树,右子树下最高的子树应该是右子树。如果新增节点后不满足这个条件,就要先对左子树左旋,或者对右子树右旋,来满足这个条件。
代码实现
from typing import Optional
class AVLTreeNode:
"""树节点
"""
def __init__(self, value: int, parent: 'AVLTreeNode') -> None:
self.value = value
self.parent = parent
self.left: Optional['AVLTreeNode'] = None
self.right: Optional['AVLTreeNode'] = None
@property
def height(self) -> int:
"""子树高度
Returns:
int: 子树高度
"""
return max(self._left_height, self._right_height)+1
@property
def _left_height(self):
return self.left.height if self.left is not None else 0
@property
def _right_height(self):
return self.right.height if self.right is not None else 0
@property
def balance(self) -> bool:
"""是否平衡
Returns:
bool: 是否平衡
"""
return abs(self._left_height-self._right_height) <= 1
def right_rotate(self):
"""节点右旋
"""
if self.left is None:
raise Exception('can not rotate tree with empty left node')
# 旧的根成为右节点
# 旧的根的左节点成为新的根
# 新的根的右节点变成旧的根的左节点
# 旧的根变成新的根的右节点
old_root = self
new_root = old_root.left
old_root.left = new_root.right
new_root.right = old_root
# 新根替换旧根
if old_root.parent is not None:
if old_root.parent.left == old_root:
old_root.parent.left = new_root
else:
old_root.parent.right = new_root
new_root.parent = old_root.parent
old_root.parent = new_root
if old_root.left is not None:
old_root.left.parent = old_root
def left_rotate(self):
"""节点左旋
"""
if self.right is None:
raise Exception('can not rotate tree with empty right node')
# 旧的根成为左节点
# 旧的根的右节点成为新的根
# 新的根的左节点作为旧的根的右子树
# 旧的根变成新的根的左子树
old_root = self
new_root = self.right
old_root.right = new_root.left
new_root.left = old_root
# 新根替换旧根
if old_root.parent is not None:
if old_root.parent.left == old_root:
old_root.parent.left = new_root
else:
old_root.parent.right = new_root
new_root.parent = old_root.parent
old_root.parent = new_root
if old_root.right is not None:
old_root.right.parent = old_root
assert new_root.right.value > new_root.value
assert new_root.left.value < new_root.value
def _rebalance(self):
if self.balance:
return
if self._left_height > self._right_height:
# 如果最高的子树是左子树的右子树,先对左子树左旋
if self.left.left is not None \
and self.left.right is not None \
and self.left.left.height < self.left.right.height:
self.left.left_rotate()
self.right_rotate()
else:
# 如果最高的子树是右子树的左子树,先对右子树右旋
if self.right.right is not None \
and self.right.left is not None \
and self.right.right.height < self.right.left.height:
self.right.right_rotate()
self.left_rotate()
def insert(self, value: int) -> None:
"""插入新节点
Args:
value (int): 要插入的数据
"""
if self.value > value:
if self.left is None:
self.left = AVLTreeNode(value, self)
else:
self.left.insert(value)
elif self.value < value:
if self.right is None:
self.right = AVLTreeNode(value, self)
else:
self.right.insert(value)
else:
return
self._rebalance()
def search(self, value: int) -> bool:
"""搜索值
Args:
value (int): 待搜索的值
Returns:
bool: 值是否存在
"""
if self.value == value:
return True
elif self.value > value and self.left is not None:
return self.left.search(value)
elif self.value < value and self.right is not None:
return self.right.search(value)
else:
return False
class AVLTree:
"""AVL tree
"""
def __init__(self) -> None:
self.root: Optional[AVLTreeNode] = None
@property
def height(self):
"""AVL树高度
Returns:
int: 树高度
"""
if self.root is not None:
return self.root.height
return 0
@property
def balance(self) -> bool:
"""树是否平衡
Returns:
bool: 树是否平衡
"""
if self.root is not None:
return self.root.balance
return True
def insert(self, value: int):
"""insert new value
Args:
value (int): new value
"""
if self.root is None:
self.root = AVLTreeNode(value, None)
else:
self.root.insert(value)
# AVL 树旋转后根节点可能不再是现在这个节点,需要重新寻找根节点
top = self.root
while top.parent is not None:
top = top.parent
self.root = top
def search(self, value: int) -> bool:
"""search a value
Args:
value (int): searching value
"""
if self.root is None:
return False
return self.root.search(value)
总结
AVL树只要理解和左右旋转的方法和作用,就不难理解左右旋转与双旋转的意义了。
单次旋转的目的都是将两侧子树,一颗子树高度+1,一颗子树高度-1,将高度相差2的两颗子树重新平衡。
单次旋转的限制是只能降低子树中一颗子树的高度,左子树的左子树或右子树的右子树,所以一旦出现左右子树中最高的子树不是左-左或右-右,单次旋转就不能重新平衡。对这种情况,先旋转子树,令左-左或右-右成为最高的子树后,再对根节点旋转,就能重新平衡了。