CNN卷积神经网络
概述
卷积神经网络是一种神经网络,它主要用来处理图像和语音。
全连接神经网络在图像处理任务中存在缺陷,因其输入是一个向量,丢失了图像的空间特征,如相邻像素之间的关系。 在图像处理任务中,卷积层可以提取图像的空间特征,如相邻像素之间的关系。
典型的 CNN 卷积神经网络如图所示。
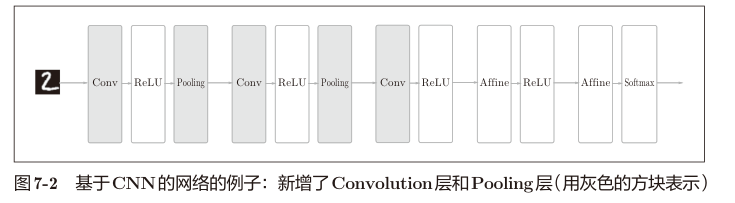
卷积层
书中卷积定义为:图像处理中的滤波器运算。
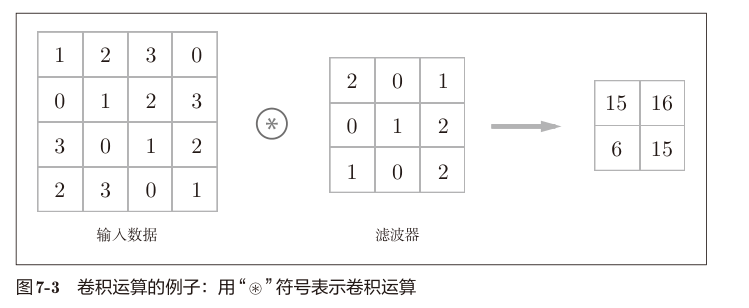
输入数据为三维图像信息(channel,height,width),也称特征图, 定义卷积核(或者卷积滤波器)为二维矩阵, 卷积核的大小为(channel,kernel_height,kernel_width), 卷积核的移动步长为stride, 卷积核的填充为padding。 矩阵元素的值就是卷积核的权重。
想象将卷积核从图像的左上角开始,向右移动stride个像素,然后从卷积核的左上角开始,向下移动stride个像素,重复这个过程,直到卷积核到达图像的右下角。
对卷积核覆盖的区域,与卷积核矩阵对位元素相乘,然后求和,得到卷积结果。
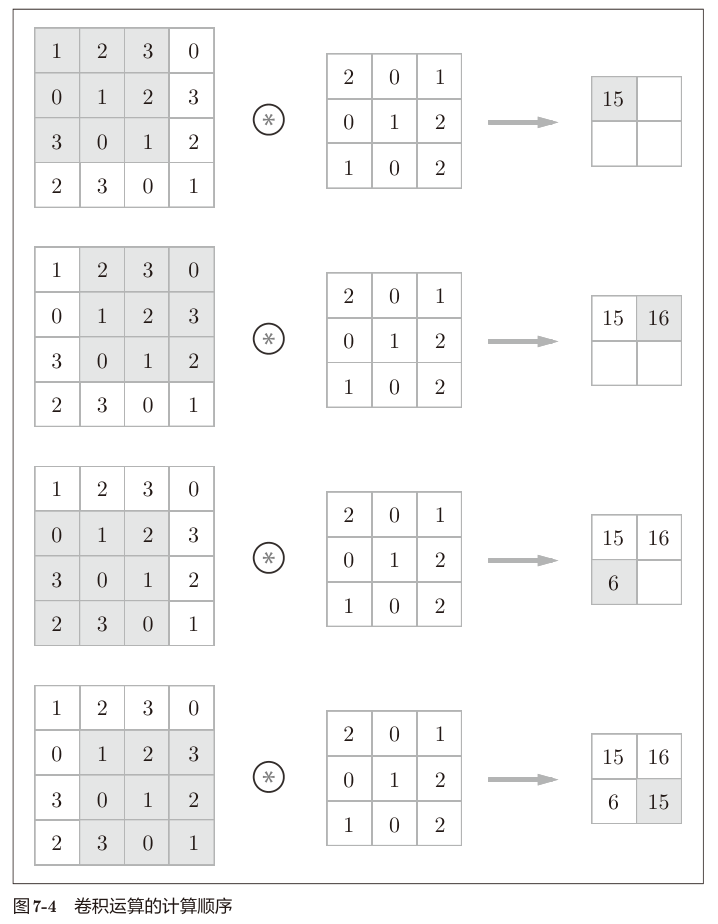
对于多通道图像的卷积如下。
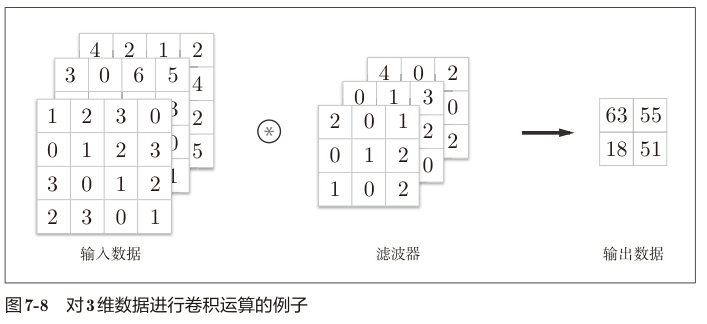
卷积层同样也有偏置值。
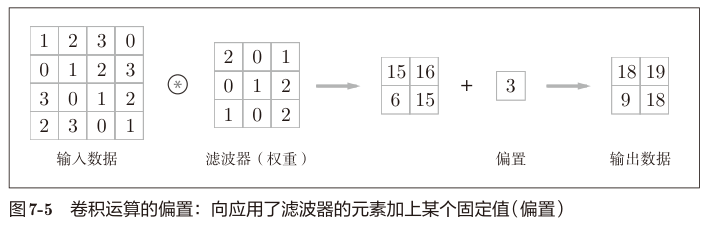
卷积核的填充,指的是对输入图像四周的填充,目的是为了保证卷积结果的大小不变。
无填充的情况下,应用卷积操作后,卷积结果的大小为:height-kernel_height+1, width-kernel_width+1。 多应用几次卷积操作,卷积结果的大小会越来越小。在某个时刻,卷积结果的大小会等于1,此时无法再继续应用卷积操作。
填充的作用是,保持卷积结果的大小和原输入图像大小一致。可以保持空间大小不变的情况下把数据传给下一层。
其次是步幅stride,步幅大小影响卷积结果的大小。 带padding时,步幅大小为1,卷积结果的大小不变。 步幅大小为2时,卷积结果的大小变为原来的1/2。 步幅大小为3时,卷积结果的大小变为原来的1/3。
书中提供了一条公式:

以上。对于多通道图像卷积我们会发现,卷积结果的通道数固定是1,也就是输出空间对比输入空间还是缩小了。 如果我们需要输出多个通道的结果,则可以定义多个卷积核。卷积核数量等于输出通道数。
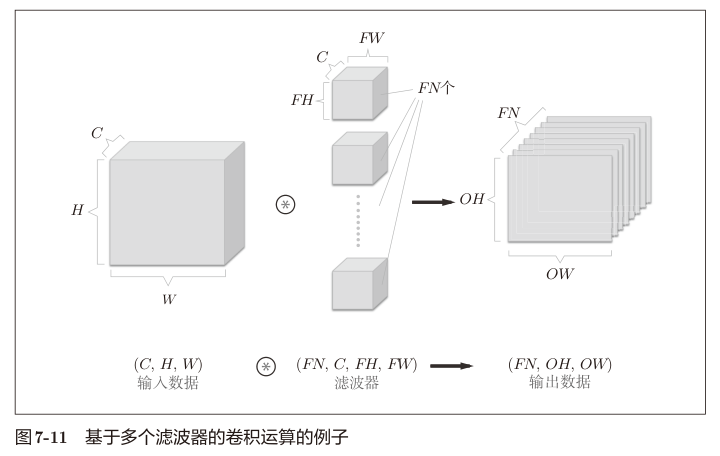
注意多个卷积核的情况下,偏置是一个三维的张量 (FN,1,1)。
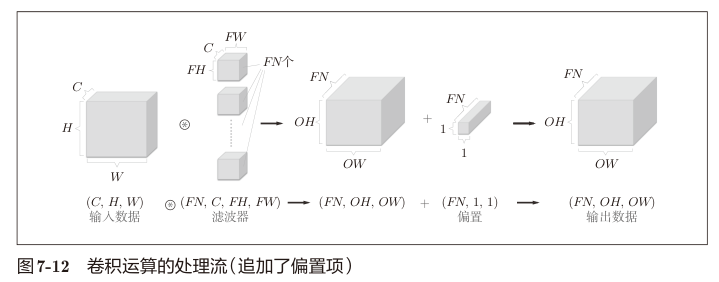
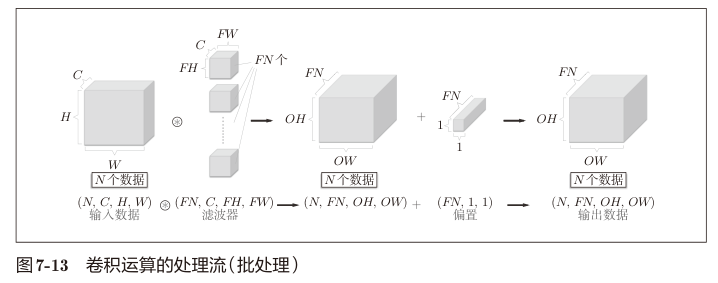
卷积层批处理
卷积层的批处理就是给输入的特征图再增加一个维度,批样本数量 N。
之后的处理就是对这个 N 个特征图进行卷积操作,输出N个数据。
卷积层的实现
im2col
首先定义卷积层的参数,即上面提到的四维数组 (卷积核数量FN,通道数量C,卷积核高度FH,卷积核宽度FW),使用 numpy.ndarray 实现。
输入同样是四维数组, 定义为 (批样本数N,通道数量C,特征图高度H,特征图宽度W)。
卷积运算的实现用的是 im2col。其基本思路是把每个卷积运算都转换为一个矩阵的运算。参考文章 im2col方法实现卷积算法。
例如对下面的 44 的输入 X,应用 33 的卷积核 W,我们需要对输入X做四次卷积运算。我们先提取四次卷积运算的参数 $X^i$
输入 X 如下
| / | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | x(1,1) | x(1,2) | x(1,3) | x(1,4) |
| 2 | x(2,1) | x(2,2) | x(2,3) | x(2,4) |
| 3 | x(3,1) | x(3,2) | x(3,3) | x(3,4) |
| 4 | x(4,1) | x(4,2) | x(4,3) | x(4,4) |
第一次卷积(X的坐标1,1到3,3的卷积运算)的参数 $X^1$ 是输入 $X$ 的一部分。
| / | 1 | 2 | 3 |
|---|---|---|---|
| 1 | x(1,1) | x(1,2) | x(1,3) |
| 2 | x(2,1) | x(2,2) | x(2,3) |
| 3 | x(3,1) | x(3,2) | x(3,3) |
将这个矩阵平坦化,转换成一个行向量,得到下面的向量。
| / | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | x(1,1) | x(1,2) | x(1,3) | x(2,1) | x(2,2) | x(2,3) | x(3,1) | x(3,2) | x(3,3) |
卷积核 W 的定义如下。
| / | 1 | 2 | 3 |
|---|---|---|---|
| 1 | w(1,1) | w(1,2) | w(1,3) |
| 2 | w(2,1) | w(2,2) | w(2,3) |
| 3 | w(3,1) | w(3,2) | w(3,3) |
同样平坦化为行向量,然后转置成只有一个列的矩阵,得到下面的矩阵。
| / | 1 |
|---|---|
| 1 | w(1,1) |
| 2 | w(1,2) |
| 3 | w(1,3) |
| 4 | w(2,1) |
| 5 | w(2,2) |
| 6 | w(2,3) |
| 7 | w(3,1) |
| 8 | w(3,2) |
| 9 | w(3,3) |
这样一个卷积运算就可以转换为一个简单的矩阵乘法运算。
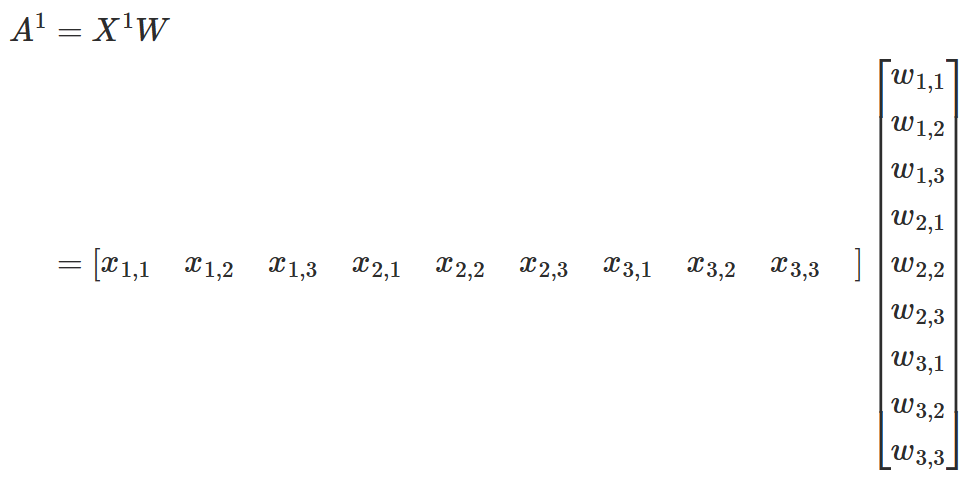
然后全局地看,4x4 特征图对 3x3 卷积核的卷积操作,可以视为四次上述矩阵运算的结果,定义为
$$ \begin{aligned} A &= \begin{bmatrix} A^1 \ A^2 \ A^3 \ A^4 \end{bmatrix} \ &= \begin{bmatrix} X^1 \ X^2 \ X^3 \ X^4 \end{bmatrix} W\ &= \begin{bmatrix} X^1 W \ X^2 W\ X^3 W\ X^4 W\end{bmatrix} \ \end{aligned} $$
也就是四次卷积,我们可以提取出输入特征图子集构成输入矩阵 X,合并成一个矩阵乘法运算 $A=XW$。
我们尝试用 python 验证下计算过程是否符合预期。
import numpy as np
from common.util import im2col
# 输入特征图 (N,C,H,W)=(1,1,4,4)
X = np.array([[
[[1.0, 2.0, 3.0, 4.0],
[5.0, 6.0, 7.0, 8.0],
[9.0, 10., 11., 12.],
[13., 14., 15., 16.]],
]])
# 卷积核 (FN,C,FH,FW)=(1,1,3,3)
W = np.array([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])
# im2col 卷积参数为 3x3 步长1 无填充
cols = im2col(X, 3, 3, 1, 0)
# 得到矩阵 [X^1 X^2 X^3 X^4]
print('X =', cols)
# 平坦化W再转置
Wt = np.array([W.flatten()]).T
print('W =', Wt)
# 点乘!
A = np.dot(cols, Wt)
# 结果平坦化后再 reshape 成 2x2
At = A.flatten().reshape((2, 2))
print(f'A = {At}')
# 验算过程。ndarray 切片取矩阵子集,平坦化后和卷积核W对位相乘求和。
a1 = np.sum(X[0, 0, :3, :3].flatten() * W.flatten())
a2 = np.sum(X[0, 0, :3, 1:4].flatten() * W.flatten())
a3 = np.sum(X[0, 0, 1:4, :3].flatten() * W.flatten())
a4 = np.sum(X[0, 0, 1:4, 1:4].flatten() * W.flatten())
expected = np.array([[a1, a2],
[a3, a4]])
print(f'expected {expected}')
assert np.allclose(At, expected)
X = [[ 1. 2. 3. 5. 6. 7. 9. 10. 11.]
[ 2. 3. 4. 6. 7. 8. 10. 11. 12.]
[ 5. 6. 7. 9. 10. 11. 13. 14. 15.]
[ 6. 7. 8. 10. 11. 12. 14. 15. 16.]]
W = [[1.]
[2.]
[3.]
[4.]
[5.]
[6.]
[7.]
[8.]
[9.]]
A = [[348. 393.]
[528. 573.]]
expected [[348. 393.]
[528. 573.]]
对于多通道的输入,卷积核也是多通道的。多通道特征图的卷积操作和单通道的卷积操作类似。只需要把各通道的输入上下拼接成矩阵得到 $X^1$ ,然后同样平坦化。
对于多通道卷积核 W 也是一样操作,将各通道的 W 上下拼接得到矩阵 W ,然后平坦化再转置得到新的单列矩阵 $W^T$。
如下:
输入特征图通道1
| / | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | x(1,1,1) | x(1,1,2) | x(1,1,3) | x(1,1,4) |
| 2 | x(1,2,1) | x(1,2,2) | x(1,2,3) | x(1,2,4) |
| 3 | x(1,3,1) | x(1,3,2) | x(1,3,3) | x(1,3,4) |
| 4 | x(1,4,1) | x(1,4,2) | x(1,4,3) | x(1,4,4) |
输入特征图通道2
| / | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | x(2,1,1) | x(2,1,2) | x(2,1,3) | x(2,1,4) |
| 2 | x(2,2,1) | x(2,2,2) | x(2,2,3) | x(2,2,4) |
| 3 | x(2,3,1) | x(2,3,2) | x(2,3,3) | x(2,3,4) |
| 4 | x(2,4,1) | x(2,4,2) | x(2,4,3) | x(2,4,4) |
则创建的 $X^1$ 矩阵为:
| / | 1 | 2 | 3 |
|---|---|---|---|
| 1 | x(1,1,1) | x(1,1,2) | x(1,1,3) |
| 2 | x(1,2,1) | x(1,2,2) | x(1,2,3) |
| 3 | x(1,3,1) | x(1,3,2) | x(1,3,3) |
| 4 | x(2,1,1) | x(2,1,2) | x(2,1,3) |
| 5 | x(2,2,1) | x(2,2,2) | x(2,2,3) |
| 6 | x(2,3,1) | x(2,3,2) | x(2,3,3) |
类似的,创建的 $W^T$ 矩阵为:
| / | 1 | 2 | 3 |
|---|---|---|---|
| 1 | w(1,1,1) | w(1,1,2) | w(1,1,3) |
| 2 | w(1,2,1) | w(1,2,2) | w(1,2,3) |
| 3 | w(1,3,1) | w(1,3,2) | w(1,3,3) |
| 4 | w(2,1,1) | w(2,1,2) | w(2,1,3) |
| 5 | w(2,2,1) | w(2,2,2) | w(2,2,3) |
| 6 | w(2,3,1) | w(2,3,2) | w(2,3,3) |
多通道卷积核输出是单通道的,计算和单通道卷积核差异不大。 我们接着考虑多个卷积核的情况,即完整的卷积层 Conv(FN,C,FH,FW) 使用 im2col 实现卷积运算的思路。
依然很简单,考虑 $W^T=\begin{bmatrix}W_1 & W_2\end{bmatrix}$,也就是第一个卷积核元素放在 $W^T$ 的第一列,第二个卷积核放在第二列...
最后依然是简单的矩阵乘法运算。
为什么可以这样?考虑矩阵点积的定义,X 矩阵的 行是单个卷积操作的输入特征图子集,$W^T$ 矩阵的列 是单个卷积操作的卷积核权重。 $XW$ 运算将 X 的行乘 W 的列然后求和,即完成一个卷积运算。$W^T$ 有多个列的情况下,X的行逐个和列运算,相当于多个卷积核在同一个输入特征图上进行卷积。 最终输出的每个列,对应一个卷积核的结果。
完整的卷积层看完,最后是批量化。
批量化依然是同样的思路,例如对输入(2,2,4,4),卷积参数(2,2,3,3),把样本1和样本2的 $X^1$ 纵向拼接得到 $\begin{bmatrix}X_{1,1} \ X_{1,2} \ X_{1,3} \ X_{1,4} \ X_{2,1} \ X_{2,2} \ X_{2,3} \ X_{2,4} \ \end{bmatrix}$ ,其中 $X_{1,2}$ 表示样本 1 的第 2 步卷积操作的输入特征图子集。
创建出矩阵 $X$ 之后和卷积核矩阵 $W$ 求点积即可。
我们实现一下完整的卷积层 Conv(FN,C,FH,FW) 正向传播运算。
import numpy as np
from common.util import im2col
from common.layers import Convolution
class Conv:
def __init__(self, fn: int, c: int, fh: int, fw: int, stride: int, padding: int, bias: float):
self.fn = fn
self.c = c
self.fh = fh
self.fw = fw
self.stride = stride
self.padding = padding
self.b = bias
self._kernels = np.random.randn(fn, c, fh, fw)
self._w_columns = np.reshape(self.kernels, (self.fn, -1)).T
self.x_columns = None
@property
def kernels(self):
return self._kernels
@kernels.setter
def kernels(self, k):
self._kernels = k
self._w_columns = np.reshape(self.kernels, (self.fn, -1)).T
@property
def w_columns(self):
return self._w_columns
def forward(self, x):
n, c, h, w = x.shape
self.x_columns = im2col(x, self.fh, self.fw, self.stride, self.padding)
out = np.dot(self.x_columns, self.w_columns) + self.b
out_h = 1 + int((h + 2 * self.padding - self.fh) / self.stride)
out_w = 1 + int((w + 2 * self.padding - self.fw) / self.stride)
out = out.reshape(n, out_h, out_w, -1).transpose(0, 3, 1, 2)
return out
# 批量输入特征图,(2,2,4,4)
x = np.array([
[
[[1.0, 2.0, 3.0, 4.0], # 样本 1 通道 1
[5.0, 6.0, 7.0, 8.0],
[9.0, 10., 11., 12.],
[13., 14., 15., 16.]],
[[1.0, 2.0, 3.0, 4.0], # 样本 1 通道 2
[5.0, 6.0, 7.0, 8.0],
[9.0, 10., 11., 12.],
[13., 14., 15., 16.]],
],
[
[[1.0, 2.0, 3.0, 4.0], # 样本 2 通道 1
[5.0, 6.0, 7.0, 8.0],
[9.0, 10., 11., 12.],
[13., 14., 15., 16.]],
[[1.0, 2.0, 3.0, 4.0], # 样本 2 通道 2
[5.0, 6.0, 7.0, 8.0],
[9.0, 10., 11., 12.],
[13., 14., 15., 16.]],
],
])
c = Conv(2, 2, 3, 3, 1, 0, 1.0)
# 初始化一个简单的卷积核 (2,2,3,3)
c.kernels = np.array([
[
[[1., 1., 1.], # 卷积核 1 通道 1
[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.], # 卷积核 1 通道 2
[1., 1., 1.],
[1., 1., 1.]],
],
[
[[1., 1., 1.], # 卷积核 2 通道 1
[1., 1., 1.],
[1., 1., 1.]],
[[1., 1., 1.], # 卷积核 2 通道 2
[1., 1., 1.],
[1., 1., 1.]],
],
])
a = c.forward(x)
expected = Convolution(c.kernels, c.b).forward(x)
print(a)
assert np.allclose(a, expected), 'forward result not equals to expected'
[[[[109. 127.]
[181. 199.]]
[[109. 127.]
[181. 199.]]]
[[[109. 127.]
[181. 199.]]
[[109. 127.]
[181. 199.]]]]
文中实现最为魔术的地方就是对 out 的 reshape 和 transpose 了。
要理解 out = out.reshape(n, out_h, out_w, -1).transpose(0, 3, 1, 2) 这句代码需要从批量卷积,点积结果矩阵的构成说起。
我们知道单张输入特征图 (C,H,W) 在点积运算中体现为矩阵 X 的一行,单个卷积核 (C,FH,FW) 在点积运算中体现为矩阵 W 的一列。 而最终结果矩阵 A 的点是单张特征图对单个卷积核的卷积结果,矩阵 A 的一个行对应输入的一张特征图,矩阵 A 的一个列则对应一个卷积核。
而我们预期的卷积层输出结果是 (N,C,H,W) 这样一个四维数组,可以作为下一个卷积层的输入。结果矩阵 A 则是 (样本数N,样本多个卷积核的卷积结果C)。
注意 A 的行实际是多个卷积核卷积结果横向连接起来的,单个卷积核的结果又是 (H,W) 矩阵平坦化组成的。也就是:
| / | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | a(1,1,1) | a(1,1,2) | a(1,2,1) | a(1,2,2) | a(2,1,1) | a(2,1,2) | a(2,2,1) | a(2,2,2) |
其中 a(1,2,1) 表示卷积核 1 输出的第 2 行第 1 列
所以我们先进行 reshape 操作,目的是把卷积结果 C 转换成矩阵形式 (H,W),因此 reshape 参数是 (n,out_h,out_w,-1), 即把矩阵 A 拆成一个四维数组 (N,OH,OW,C),此时 C 维度的大小为 2,2 个元素分别表示两个卷积核在 (N,OH,OW) 上的卷积结果。
然后进行 transpose 操作调整轴的顺序,这是个非常魔术的过程。这里直接看书中图示。
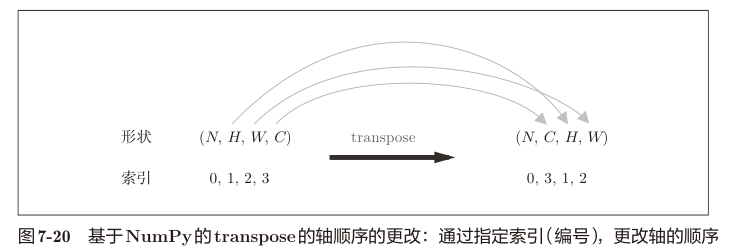
transpose 后的多维数组,我们对各个维度的解读发生了改变。如图所示,transpose 后得到的是 (N,C,OH,OW) 的数组, 其中 N 表示样本数,C 对应卷积核个数(输出通道数),OH 表示输出特征图的高度,OW 表示输出特征图的宽度。
反向传播
卷积层的反向传播书中说法是和 Affine 层的反向传播实现类似。
我们知道 Affine 层的反向传播计算公式是
$$ \begin{aligned} \frac{\partial L}{\partial X}&=\frac{\partial L}{\partial Y} \times W^T \ \frac{\partial L}{\partial W}&=\frac{\partial L}{\partial Y} \times X^T \ \end{aligned} $$
Affine 层的正向传播中,$X$ 的每个行对应样本,$W$ 的每个列对应神经元。这与 Convolution 层很相似。Convolution 层的 $W$ 每个列对应卷积核。
Convolution 层和 Affine 层正向传播的差异在于 Convolution 层的卷积核和输入特征图需要先变换成矩阵形式再参与运算。 影响是,预期传入的 dout 会是一个四维数组 (N,C,H,W) 元素对应 $W$ 矩阵元素的偏导数。 在计算前,要先把 dout 转换为矩阵形式,同样的 $W$ 也要转为矩阵,然后用 Affine 的反向传播公式求关于 $W$ 和 $X$ 的梯度。 最后将求得的关于 $X$ 的梯度转为四维数组 (N,C,H,W) 形式返回,保存 $\frac{\partial L}{\partial W}$。
我实在懒得再写一遍了,以后精读的时候可能再针对每个层都进行详细分析。迫不及待想刷完这书再去看下一本进阶了。 这里就略过反向传播的实现细节了。
池化层
池化层是缩小空间的运算。
和卷积层一样有大小和步长参数,但没有卷积核(权重),只单纯对输入压缩。
书中例子如下:
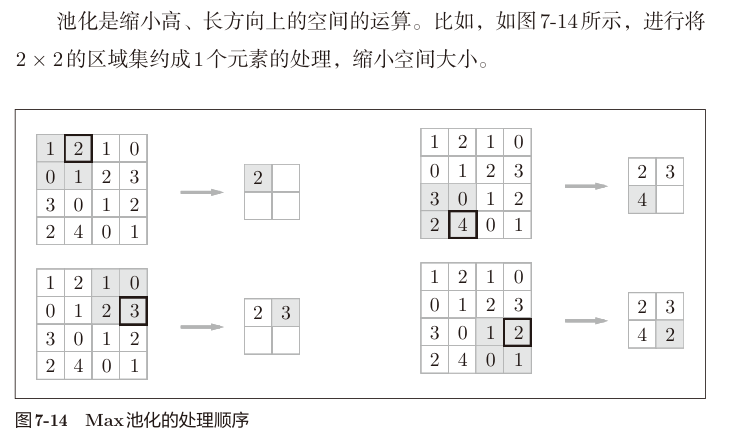
常见的池化层有最大池化和平均池化两种。最大池化是取池化窗口内的最大值,平均池化是取池化窗口内的平均值。
正向传播实现
池化层的正向传播和卷积层类似,区别在于不需要把一个样本的所有卷积参数 $X^i$ 平坦化到一个行,而是每个 $X^i$ 一个行。 把不同通道的输入特征图拆出来的 $X^i$ 上下连接起来。
书中图示比较清楚:
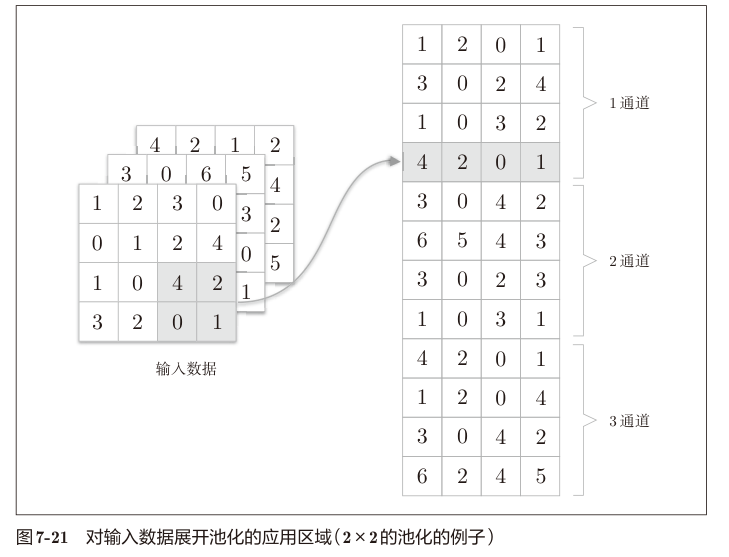
处理完之后按行池化,得到结果,再 reshape 回 4 维数组 (N,C,H,W) 即可。注意池化层输入多少通道输出就是多少通道。
反向传播实现
池化层的反向传播和 ReLU 类似,例如最大池化,除最大元素外其他元素在池化后是置0的,也就是这些位置的系数为0,偏导数为0。
具体实现细节这里略。
使用 pytorch 实现 CNN
从这里就偏离原书了,直接上 pytorch 玩玩。
import torch
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor
# Download training data from open datasets.
training_data = datasets.MNIST(root="data", train=True, download=True, transform=ToTensor())
# Download test data from open datasets.
test_data = datasets.MNIST(root="data", train=False, download=True, transform=ToTensor())
# batch size
batch_size = 64
# Create data loaders.
train_dataloader = DataLoader(training_data, batch_size=batch_size)
test_dataloader = DataLoader(test_data, batch_size=batch_size)
device = 'cuda' if torch.cuda.is_available() else 'cpu'
class MyNetwork(torch.nn.Module):
def __init__(self):
super().__init__()
self.flatten = torch.nn.Flatten()
self.linear = torch.nn.Sequential(
torch.nn.Conv2d(1, 30, 5, 1, 0),
torch.nn.ReLU(),
torch.nn.MaxPool2d(2, 1),
torch.nn.Flatten(), # 为了把 Convolution/Pooling 层的输出和 Affine 层输入串起来,需要先把 Convolution/Pooling 层输出的 4D 数组平坦化
torch.nn.Linear(15870, 100),
torch.nn.ReLU(),
torch.nn.Linear(100, 10),
torch.nn.Softmax(),
)
def forward(self, x):
return self.linear(x)
def train(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
model.train()
for batch, (X, y) in enumerate(dataloader):
X, y = X.to(device), y.to(device)
X = torch.reshape(X, (X.shape[0], 1, 28, 28))
# Compute prediction error
pred = model(X)
loss = loss_fn(pred, y)
# Backpropagation
loss.backward()
optimizer.step()
optimizer.zero_grad()
if batch % 100 == 0:
loss, current = loss.item(), (batch + 1) * len(X)
print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
def test(dataloader, model, loss_fn):
size = len(dataloader.dataset)
num_batches = len(dataloader)
model.eval()
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
X = torch.reshape(X, (X.shape[0], 1, 28, 28))
X, y = X.to(device), y.to(device)
pred = model(X)
test_loss += loss_fn(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
print(f"Test Error: \n Accuracy: {(100 * correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
n = MyNetwork().to(device)
loss_fn = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(n.parameters(), lr=0.01)
epochs = 10
for t in range(epochs):
print(f"Epoch {t + 1}\n-------------------------------")
train(train_dataloader, n, loss_fn, optimizer)
test(test_dataloader, n, loss_fn)
print("Done!")
Files already downloaded
Files already downloaded
Epoch 1
-------------------------------
F:\repos\deep-learning\venv\lib\site-packages\torch\nn\modules\module.py:1511: UserWarning: Implicit dimension choice for softmax has been deprecated. Change the call to include dim=X as an argument.
return self._call_impl(*args, **kwargs)
loss: 2.301144 [ 64/60000]
loss: 2.279937 [ 6464/60000]
loss: 2.266119 [12864/60000]
loss: 2.148455 [19264/60000]
loss: 2.036764 [25664/60000]
loss: 1.925048 [32064/60000]
loss: 1.805400 [38464/60000]
loss: 1.857848 [44864/60000]
loss: 1.821546 [51264/60000]
loss: 1.758208 [57664/60000]
Test Error:
Accuracy: 74.0%, Avg loss: 1.750762
Epoch 2
-------------------------------
loss: 1.735336 [ 64/60000]
loss: 1.741934 [ 6464/60000]
loss: 1.733680 [12864/60000]
loss: 1.639817 [19264/60000]
loss: 1.652467 [25664/60000]
loss: 1.673727 [32064/60000]
loss: 1.586213 [38464/60000]
loss: 1.640192 [44864/60000]
loss: 1.644729 [51264/60000]
loss: 1.602930 [57664/60000]
Test Error:
Accuracy: 89.7%, Avg loss: 1.588926
Epoch 3
-------------------------------
loss: 1.579320 [ 64/60000]
loss: 1.579364 [ 6464/60000]
loss: 1.563474 [12864/60000]
loss: 1.592638 [19264/60000]
loss: 1.576006 [25664/60000]
loss: 1.623149 [32064/60000]
loss: 1.539580 [38464/60000]
loss: 1.600444 [44864/60000]
loss: 1.608010 [51264/60000]
loss: 1.577690 [57664/60000]
Test Error:
Accuracy: 91.1%, Avg loss: 1.566124
Epoch 4
-------------------------------
loss: 1.552503 [ 64/60000]
loss: 1.560335 [ 6464/60000]
loss: 1.546871 [12864/60000]
loss: 1.581722 [19264/60000]
loss: 1.556692 [25664/60000]
loss: 1.605762 [32064/60000]
loss: 1.528894 [38464/60000]
loss: 1.589878 [44864/60000]
loss: 1.591401 [51264/60000]
loss: 1.566346 [57664/60000]
Test Error:
Accuracy: 91.6%, Avg loss: 1.555532
Epoch 5
-------------------------------
loss: 1.538584 [ 64/60000]
loss: 1.551226 [ 6464/60000]
loss: 1.536254 [12864/60000]
loss: 1.573621 [19264/60000]
loss: 1.545673 [25664/60000]
loss: 1.588099 [32064/60000]
loss: 1.522446 [38464/60000]
loss: 1.584719 [44864/60000]
loss: 1.583256 [51264/60000]
loss: 1.560601 [57664/60000]
Test Error:
Accuracy: 92.3%, Avg loss: 1.548232
Epoch 6
-------------------------------
loss: 1.529052 [ 64/60000]
loss: 1.545700 [ 6464/60000]
loss: 1.527557 [12864/60000]
loss: 1.567937 [19264/60000]
loss: 1.539456 [25664/60000]
loss: 1.574068 [32064/60000]
loss: 1.516613 [38464/60000]
loss: 1.580732 [44864/60000]
loss: 1.576618 [51264/60000]
loss: 1.558007 [57664/60000]
Test Error:
Accuracy: 92.7%, Avg loss: 1.542547
Epoch 7
-------------------------------
loss: 1.524871 [ 64/60000]
loss: 1.541902 [ 6464/60000]
loss: 1.519567 [12864/60000]
loss: 1.564264 [19264/60000]
loss: 1.534474 [25664/60000]
loss: 1.562087 [32064/60000]
loss: 1.507874 [38464/60000]
loss: 1.578054 [44864/60000]
loss: 1.566317 [51264/60000]
loss: 1.555856 [57664/60000]
Test Error:
Accuracy: 93.1%, Avg loss: 1.537830
Epoch 8
-------------------------------
loss: 1.522017 [ 64/60000]
loss: 1.538967 [ 6464/60000]
loss: 1.513827 [12864/60000]
loss: 1.560773 [19264/60000]
loss: 1.529202 [25664/60000]
loss: 1.553353 [32064/60000]
loss: 1.500312 [38464/60000]
loss: 1.574624 [44864/60000]
loss: 1.555169 [51264/60000]
loss: 1.554117 [57664/60000]
Test Error:
Accuracy: 93.5%, Avg loss: 1.533476
Epoch 9
-------------------------------
loss: 1.519567 [ 64/60000]
loss: 1.536195 [ 6464/60000]
loss: 1.510207 [12864/60000]
loss: 1.557672 [19264/60000]
loss: 1.524510 [25664/60000]
loss: 1.547272 [32064/60000]
loss: 1.495671 [38464/60000]
loss: 1.570410 [44864/60000]
loss: 1.543279 [51264/60000]
loss: 1.552659 [57664/60000]
Test Error:
Accuracy: 93.8%, Avg loss: 1.529591
Epoch 10
-------------------------------
loss: 1.517417 [ 64/60000]
loss: 1.534307 [ 6464/60000]
loss: 1.507608 [12864/60000]
loss: 1.554423 [19264/60000]
loss: 1.520418 [25664/60000]
loss: 1.542946 [32064/60000]
loss: 1.493244 [38464/60000]
loss: 1.565224 [44864/60000]
loss: 1.534792 [51264/60000]
loss: 1.551990 [57664/60000]
Test Error:
Accuracy: 94.0%, Avg loss: 1.526247
Done!