反向传播
本章主要是反向传播算法的学习。
计算图
计算图的概念很好理解,它本身是一种有向无环图,构成基本就是按运算符优先级分割得到的语法树。
例如 $z=xy+b$ 这条简单的公式可以表达为下面的计算图。
flowchart LR
z[z]
x[x]
y[y]
b[b]
times((*))
plus((+))
x --> times
y --> times
times --> plus
b --> plus
计算图的正向传播可以看成从入度为零的节点出发,经过计算节点时递归遍历求值输入节点,得到计算节点的输入,递归执行得到输出的过程。
例如上图,从节点 x 出发则得到下面的遍历顺序:((x y *) b +)
实质是从计算图构造出了一个后缀表达式并运算得到结果。
当然也可以反过来从出度为 0 的节点出发,反过来遍历输入节点,得到前缀表达式 (+ (* x y) b) 求值。
反向传播
反向传播利用链式法则将复杂的公式分解成多个简单公式求导。一方面简单函数求导可以直接数学推导出来得到分析解,更准确,另一方面就是极大减少了不必要的计算。
链式法则
例如求函数 $z=(x+y)^2$ 的导数。首先这条式子可以表述为两个函数的组合:$z=t^2$ 和 $t=x+y$
链式法则的定义是:
如果某个函数由复合函数表示,则该复合函数的导数可以用构成该复合函数的各个函数的导数的乘积来表示。
也就是 $z=(x+y)^2$ 的导数,可以表示为 $\frac{\partial z}{\partial t}\frac{\partial t}{\partial x}$
上面的式子约分一下可以得到 $\frac{\partial z}{\partial x}$ ,也就是原来的函数 $z=(x+y)^2$ 关于 $x$ 的导数了。
利用链式法则我们试着求原函数的解析解。
$\frac{\partial t}{\partial x}$ 的导数是 $1$ 。
$\frac{\partial z}{\partial t}$ 的导数是 $2t$ (查基本初等函数的导数公式表)
相乘得到原函数的导数 $\frac{\partial z}{\partial x}=2t=2(x+y)$,对照导数公式表无误。
结合计算图
依然是 $z=(x+y)^2$ 为例,构造计算图如下。
flowchart LR
x[x]
y[y]
plus[+]
exponential[exponential]
x --> plus
y --> plus
plus -->|底部分,命名为t| exponential
2 -->|指数部分| exponential
exponential -->|结果| z
接着从 $z$ 出发反向推导各个节点的导数。
flowchart LR
x[x]
y[y]
plus[+]
exponential[exponential]
z -->|导数:1| exponential
exponential -->|指数| 2
exponential -->|导数:1×2t| plus
plus -->|导数:1×2t×1=2x+2y| x
plus -->|导数:1×2t×1=2x+2y| y
需要注意的是,像 $t=xy$ 这样的计算节点,求导会需要输入信号。比如求 $\frac{\partial t}{\partial x}=y$,就要求保留 y 的输入才能求得导数。
尝试解书中例题,设消费税 $t=1.1$,苹果单价 $p_a=100$,橘子单价 $p_b=150$,计算图如下:
flowchart LR
苹果数量 -->|2| 苹果总价((×))
苹果单价 -->|100| 苹果总价
苹果总价 -->|200| 商品总价((+))
橘子数量 -->|3| 橘子总价((×))
橘子单价 -->|150| 橘子总价
橘子总价 -->|450| 商品总价
商品总价 -->|650| 税后总价((×))
消费税率 -->|1.1| 税后总价
税后总价 -->|715| 实际支付
现在逆推每个节点的导数。
flowchart LR
实际支付 -->|导数:1| 税后总价
税后总价 -->|导数:650| 消费税率
税后总价 -->|导数:1.1| 商品总价((+))
商品总价 -->|导数:1.1| 苹果总价((×))
商品总价 -->|导数:1.1| 橘子总价((×))
苹果总价 -->|导数:2.2| 苹果单价
苹果总价 -->|导数:110| 苹果数量
橘子总价 -->|导数:3.3| 橘子单价
橘子总价 -->|导数:165| 橘子数量
计算图的 python 实现
from typing import Optional
import numpy as np
Num = float | np.ndarray
class MulLayer:
def __init__(self) -> None:
self.x: Optional[Num] = None
self.y: Optional[Num] = None
def forward(self, x: Num, y: Num) -> Num:
self.x = x
self.y = y
return x * y
def backward(self, dout: Num) -> tuple[Num, Num]:
""" 反向传播
:return: 返回本层输入 x,y 的导数 (dx,dy)
"""
return self.y * dout, self.x * dout
class AddLayer:
def __init__(self) -> None:
pass
def forward(self, x: Num, y: Num) -> Num:
return x + y
def backward(self, dout: Num) -> tuple[Num, Num]:
return dout, dout
apple_price = 100.
apple_num = 2.
orange_price = 150.
orange_num = 3.
tax_ratio = 1.1
# 苹果总价
m1 = MulLayer()
# 橘子总价
m2 = MulLayer()
# 商品总价
a1 = AddLayer()
# 税后总价
m3 = MulLayer()
# 正向传播过程
# --------------
# 苹果总价
apple_total = m1.forward(apple_price, apple_num)
# 橘子总价
orange_total = m2.forward(orange_price, orange_num)
# 商品总价
good_total = a1.forward(apple_total, orange_total)
# 税后总价
total = m3.forward(good_total, tax_ratio)
# 反向传播过程
# --------------
# 税率和商品总价导数
good_total_diff, tax_ratio_diff = m3.backward(1)
print(f'商品总价导数:{good_total_diff}, 税率导数:{tax_ratio_diff}')
# 各项水果总价导数
apple_total_diff, orange_total_diff = a1.backward(good_total_diff)
print(f'苹果总价导数:{good_total_diff}, 橘子总价导数:{tax_ratio_diff}')
# 苹果单价和数量的导数
apple_price_diff, apple_num_diff = m1.backward(apple_total_diff)
print(f'苹果单价导数:{apple_price_diff}, 苹果数量导数:{apple_num_diff}')
orange_price_diff, orange_num_diff = m2.backward(orange_total_diff)
print(f'橘子单价导数:{orange_price_diff}, 橘子数量导数:{orange_num_diff}')
商品总价导数:1.1, 税率导数:650.0
苹果总价导数:1.1, 橘子总价导数:650.0
苹果单价导数:2.2, 苹果数量导数:110.00000000000001
橘子单价导数:3.3000000000000003, 橘子数量导数:165.0
计算层反向传播推导和实现
要用到的 numpy 特性
涉及一个 numpy.ndarray 的技巧。
import numpy as np
x = np.array([-2., -1., 0., 1., 2.])
# ndarray 直接参与比较运算,得到一个 bit mask 数组表示比较结果
mask = (x <= 0)
print(mask)
# 可以用这个 bit mask 作为索引
print(x[mask])
# 可以用这个 bit mask 索引修改原数组内容
y = x.copy()
y[mask] = 0.0
print(y)
[ True True True False False]
[-2. -1. 0.]
[0. 0. 0. 1. 2.]
ReLU 反向传播推导和实现
ReLU 层定义和实现都很简单。定义是
$$ y=\begin{cases} 0 & (x<=0)\\ x & (x>0) \end{cases} $$
可知在输入 $x<=0$ 的情况下导数为 0,其他情况导数为 1。
注意输入是 ndarray ,ReLU 传入参数是多维向量,用到上面说的技巧。
下面实现 ReLU 激活函数的
import numpy as np
class ReLULayer:
def __init__(self) -> None:
# 输入信号 <= 0 的下标数组
self.mask = None
def forward(self, x: np.ndarray, **kwargs) -> np.ndarray:
out = x.copy()
self.mask = (x <= 0)
out[self.mask] = 0
return out
def backward(self, dout: np.ndarray) -> np.ndarray:
ndout = dout.copy()
ndout[self.mask] = 0
return ndout
def optimize(self, lr):
pass
sigmoid 反向传播推导和实现
复习下 sigmoid 函数的定义。
$$ y = \frac{1}{1+{e}^{-x}} $$
手动推导下 sigmoid 函数的导数。先拆分成多个简单的基本初等函数。
$$ \begin{aligned} y &= \frac{1}{t}\\ t &= 1+z \\ z &= {e}^{a} \\ a &= -1 \times x \end{aligned} $$
然后从右往左推导各个计算节点的导数。
y=1/t 求导
$$ \begin{aligned} \frac{d}{dt}y&=\lim_{h \to 0} \frac{\frac{1}{t+h}-\frac{1}{t}}{h} \\ &=\lim_{h \to 0} \frac{\frac{t}{t(t+h)}-\frac{t+h}{t(t+h)}}{h} \\ &=\lim_{h \to 0} \frac{\frac{t-(t+h)}{t(t+h)}}{h} \\ &=\lim_{h \to 0} \frac{\frac{t-(t+h)}{t(t+h)} t(t+h)}{h t(t+h)} \\ &=\lim_{h \to 0} \frac{t-(t+h)}{h(t(t+h))} \\ &=\lim_{h \to 0} \frac{-h}{h(t^2+ht)} \\ &=\lim_{h \to 0} \frac{-1}{t^2+ht} \\ &=-\frac{1}{t^2} \\ &=-\frac{1}{(1+e^{-x})^2} \\ &=-y^2 \ \end{aligned} $$
t=1+z 求导
加法导数固定为1。
z=e^a求导
$e^a$ 的导数为 $e^a$ ,所以 $\frac{d}{da}z=e^a=e^{-x}$
a=-x求导
关于 x 的导数是 -1 。
链式法则串联起来可得原式导数分析解: $\frac{dy}{dx}=1 \times - y^2 \times e^{-x} \times -1 = y^2e^{-x}$
进一步化简可以展开 $y^2e^{-x}$,得到
$$ \begin{aligned} y^2e^{-x} &= \frac{e^{-x}}{(1+e^{-x})^2} \\ &= \frac{1}{1+e^{-x}} \frac{e^{-x}}{1+e^{-x}} \\ &= \frac{1}{1+e^{-x}} \frac{(1+e^{-x})-1}{1+e^{-x}} \\ &= \frac{1}{1+e^{-x}} (\frac{1+e^{-x}}{1+e^{-x}} - \frac{1}{1+e^{-x}}) \\ &= y(1-y) \end{aligned} $$
import numpy as np
class SigmoidLayer:
def __init__(self) -> None:
self.y = None
def forward(self, x, **kwargs):
self.y = 1.0 / (1.0 + np.exp(-x))
return self.y
def backward(self, dout):
return self.y * (1.0 - self.y) * dout
def optimize(self, lr):
pass
affine 层反向传播推导和实现
affine 层直译仿射层,指的是 $y=wx+b$ ,这条式子在几何领域称为仿射变换因此称仿射层。
affine 层正向传播的计算可以画出下面的图
flowchart LR
x1[x1]
x2[x2]
subgraph neuro1
w11[w11]
w12[w12]
end
subgraph neuro2
w21[w21]
w22[w22]
end
subgraph neuro3
w31[w31]
w32[w32]
end
w11 --> x1w11((*))
w12 --> x1w12((*))
w21 --> x1w21((*))
w22 --> x1w22((*))
w31 --> x1w31((*))
w32 --> x1w32((*))
x1 ---> x1w11((*))
x2 ---> x1w12((*))
x1 ---> x1w21((*))
x2 ---> x1w22((*))
x1 ---> x1w31((*))
x2 ---> x1w32((*))
x1w11 & x1w12 --> a1((+))
x1w21 & x1w22 --> a2((+))
x1w31 & x1w32 --> a3((+))
a1 & a2 & a3 --> a
已知
$$ \begin{aligned} a &= \begin{bmatrix} a_1 & a_2 & a_3 \end{bmatrix}\\ x &= \begin{bmatrix} x_1 & x_2 \end{bmatrix}\\ w &= \begin{bmatrix} w_{11} & w_{21} & w_{31}\\ w_{12} & w_{22} & w_{32} \end{bmatrix}\\ \frac{\partial a}{\partial w} &= \begin{bmatrix} x_1 & x_1 & x_1\\ x_2 & x_2 & x_2 \end{bmatrix} \end{aligned} $$
不难发现,在 $w$ 中,第 $i$ 行的元素的偏导数,就是 $x$ 的第 $i$ 列输入。
所以求 $w$ 的偏导数就是将 $x$ 转置(列旋转为行,第 $i$ 列转为第 $i$ 行),然后把这个矩阵改成每个行含 n 个相同的列,n为神经元个数。
转置很好处理,后面将每个行改成n个列的过程可以表述成 $X^T\frac{\partial a}{\partial a}$,其中 $\frac{\partial a}{\partial a}=\begin{bmatrix}1 & 1 & 1\end{bmatrix}$
从计算图角度看就是 a 出发分别求每个神经元输入权重的偏导数,然后排列成和权重矩阵一样的形状。
手动计算过程如下。
$$ \begin{aligned} X^T &= \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\\ \frac{\partial L}{\partial Y} &= \begin{bmatrix} 1 & 1 & 1 \end{bmatrix}\\ X^T \frac{\partial L}{\partial Y} &= \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \end{bmatrix}\\ &= \begin{bmatrix} x_1 & x_1 & x_1 \\ x_2 & x_2 & x_2 \end{bmatrix} \end{aligned} $$
输入 $x$ 有多行的情况下则是:
$$ \begin{aligned} a &= \begin{bmatrix} a\_{11} & a\_{12} & a\_{13} \\ a\_{21} & a\_{22} & a\_{23} \end{bmatrix} \\ x &= \begin{bmatrix} x\_{11} & x\_{12} \\ x\_{21} & x\_{22} \end{bmatrix} \\ w &= \begin{bmatrix} w\_{11} & w\_{21} & w\_{31} \\ w\_{12} & w\_{22} & w\_{32} \end{bmatrix} \\ X^T &= \begin{bmatrix} x\_{11} x\_{21} \\ x\_{12} x\_{22} \end{bmatrix}\\ \frac{\partial L}{\partial Y} &= \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} \\ X^T \frac{\partial L}{\partial Y} &= \begin{bmatrix} x\_{11} x\_{12} \\ x\_{21} x\_{22} \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} \\ &= \begin{bmatrix} x\_{11}+x\_{12} & x\_{11}+x\_{12} & x\_{11}+x\_{12} \\ x\_{21}+x\_{22} & x\_{21}+x\_{22} & x\_{21}+x\_{22} \\ \end{bmatrix} \\ \end{aligned} $$
也就是输入多个样本得到的 $w$ 的偏导数之和。
最后是考虑偏置 $b$ ,书中实现是 $\frac{\partial L}{\partial Y}$ 按列求和,其实和上面的多个样本的 $w$ 偏导数之和一样。 如果把偏置理解为输入始终为 1 的神经元,加入上面的式子推导,可以得到最终多出来的行其实就等于原 $\frac{\partial L}{\partial Y}$ 各列元素之和。
$$ \begin{aligned} a &=\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{bmatrix}\\ x &=\begin{bmatrix} x_{11} & x_{12} & 1\\ x_{21} & x_{22} & 1 \end{bmatrix}\\ w &=\begin{bmatrix} w_{11} & w_{21} & w_{31}\\ w_{12} & w_{22} & w_{32}\\ b & b & b \end{bmatrix}\\ X^T &= \begin{bmatrix} x_{11} & x_{21}\\ x_{12} & x_{22}\\ 1 & 1 \end{bmatrix}\\ \frac{\partial L}{\partial Y} &=\begin{bmatrix} \frac{\partial L}{\partial Y_{11}} & \frac{\partial L}{\partial Y_{12}} & \frac{\partial L}{\partial Y_{13}}\\ \frac{\partial L}{\partial Y_{21}} & \frac{\partial L}{\partial Y_{22}} & \frac{\partial L}{\partial Y_{23}} \end{bmatrix}\\ X^T \frac{\partial L}{\partial Y} &=\begin{bmatrix} x_{11} & x_{12} \\ x_{12} & x_{22}\\ 1 & 1\\ \end{bmatrix} \begin{bmatrix} \frac{\partial L}{\partial Y_{11}} & \frac{\partial L}{\partial Y_{12}} & \frac{\partial L}{\partial Y_{13}}\\ \frac{\partial L}{\partial Y_{21}} & \frac{\partial L}{\partial Y_{22}} & \frac{\partial L}{\partial Y_{23}} \end{bmatrix}\\ &=\begin{bmatrix} \frac{\partial L}{\partial Y_{11}} x_{11}+\frac{\partial L}{\partial Y_{12}} x_{12} & \frac{\partial L}{\partial Y_{11}} x_{11}+\frac{\partial L}{\partial Y_{12}} x_{12} & \frac{\partial L}{\partial Y_{11}} x_{11}+\frac{\partial L}{\partial Y_{12}} x_{12}\\ \frac{\partial L}{\partial Y_{21}} x_{21}+\frac{\partial L}{\partial Y_{22}} x_{22} & \frac{\partial L}{\partial Y_{21}} x_{21}+\frac{\partial L}{\partial Y_{22}} x_{22} & \frac{\partial L}{\partial Y_{21}} x_{21}+\frac{\partial L}{\partial Y_{22}} x_{22}\\ \frac{\partial L}{\partial Y_{11}} + \frac{\partial L}{\partial Y_{21}} & \frac{\partial L}{\partial Y_{12}} + \frac{\partial L}{\partial Y_{22}} & \frac{\partial L}{\partial Y_{13}} + \frac{\partial L}{\partial Y_{23}}\\ \end{bmatrix}\\ \end{aligned} $$
下面就按上面的推导实现下,注意 affine 层前还可以连接别的层,反向传播并不是在 affine 层终止的。 书中 backward 返回的结果会作为上一层的 dout,所以 affine 层保存了 dw 而返回的是 dx。
class AffineLayer:
def __init__(self, w: np.ndarray, b: np.ndarray) -> None:
self.w = w
self.b = b
self.x: Optional[np.ndarray] = None
self.dw: Optional[np.ndarray] = None
self.db: Optional[np.ndarray] = None
def forward(self, x: np.ndarray, **kwargs):
self.x = x
out = np.dot(self.x, self.w) + self.b
return out
def backward(self, dout: np.ndarray):
dx = np.dot(dout, self.w.T)
self.dw = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dx
def optimize(self, lr):
if self.dw is not None and self.w is not None:
self.w -= lr * self.dw
softmax-with-loss 实现
回顾 softmax 函数的定义
$$ y_k=\frac{exp(a_k)}{\sum_{i=1}^{n} exp(a_i)} $$
其中 $k$ 表示 softmax 输出下标,$i$ 表示 softmax 输入的下标,输入总数为 $n$。
题中的 with-loss 意指这一层还包含一个损失函数,书中是交叉熵损失函数,定义如下。
$$ L=-\sum_{k}t_k \log_{e}y_k $$
书中计算图如下
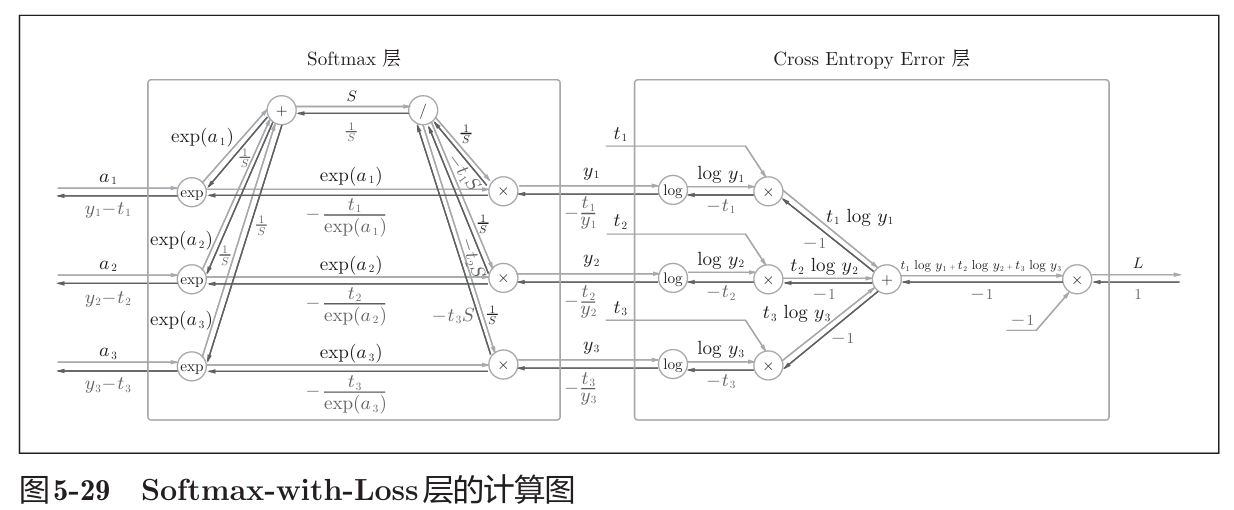
计算图反向传播结果:
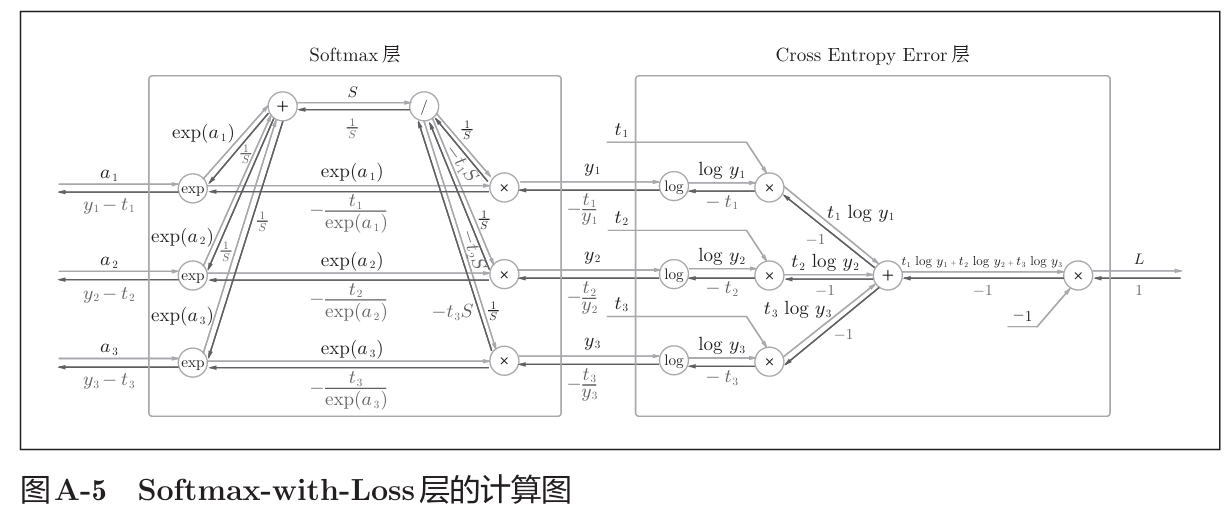
计算过程在书中附录A,如下。
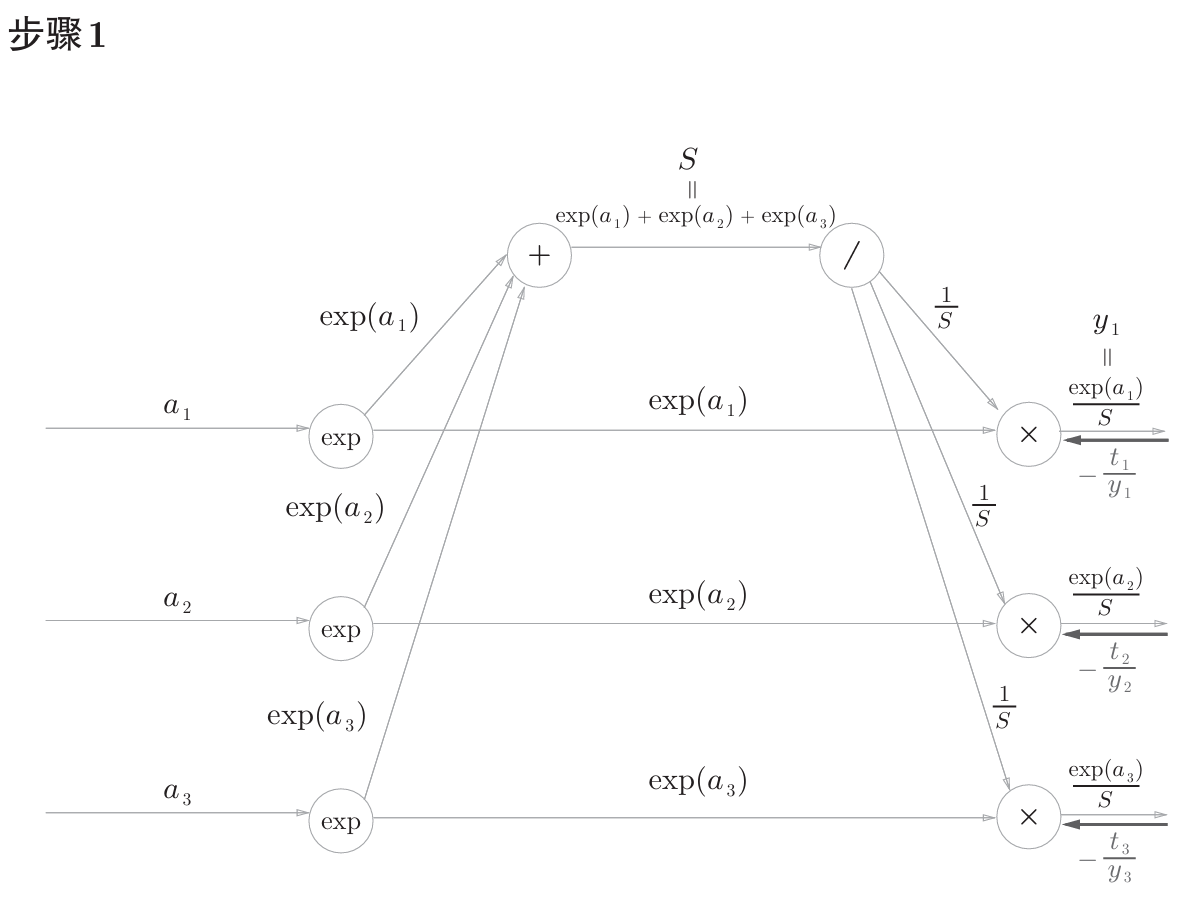
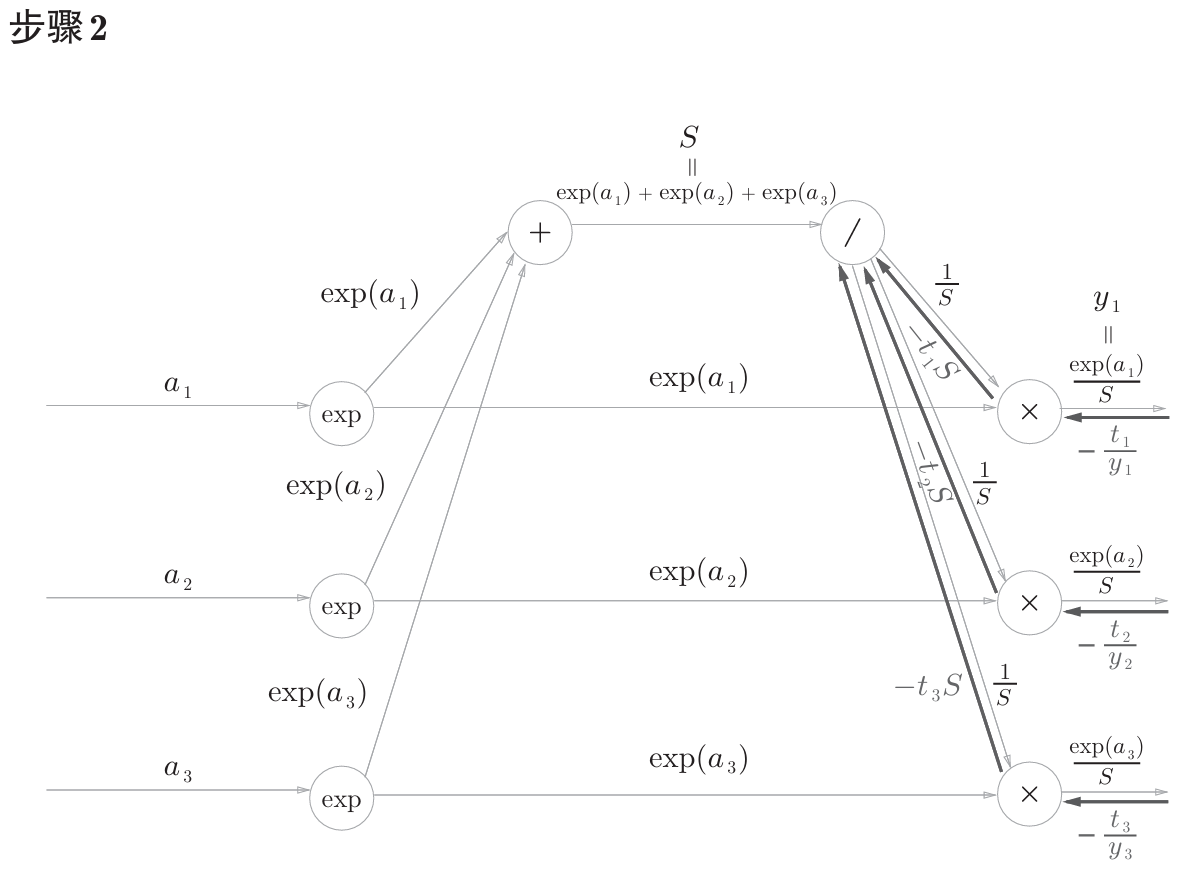
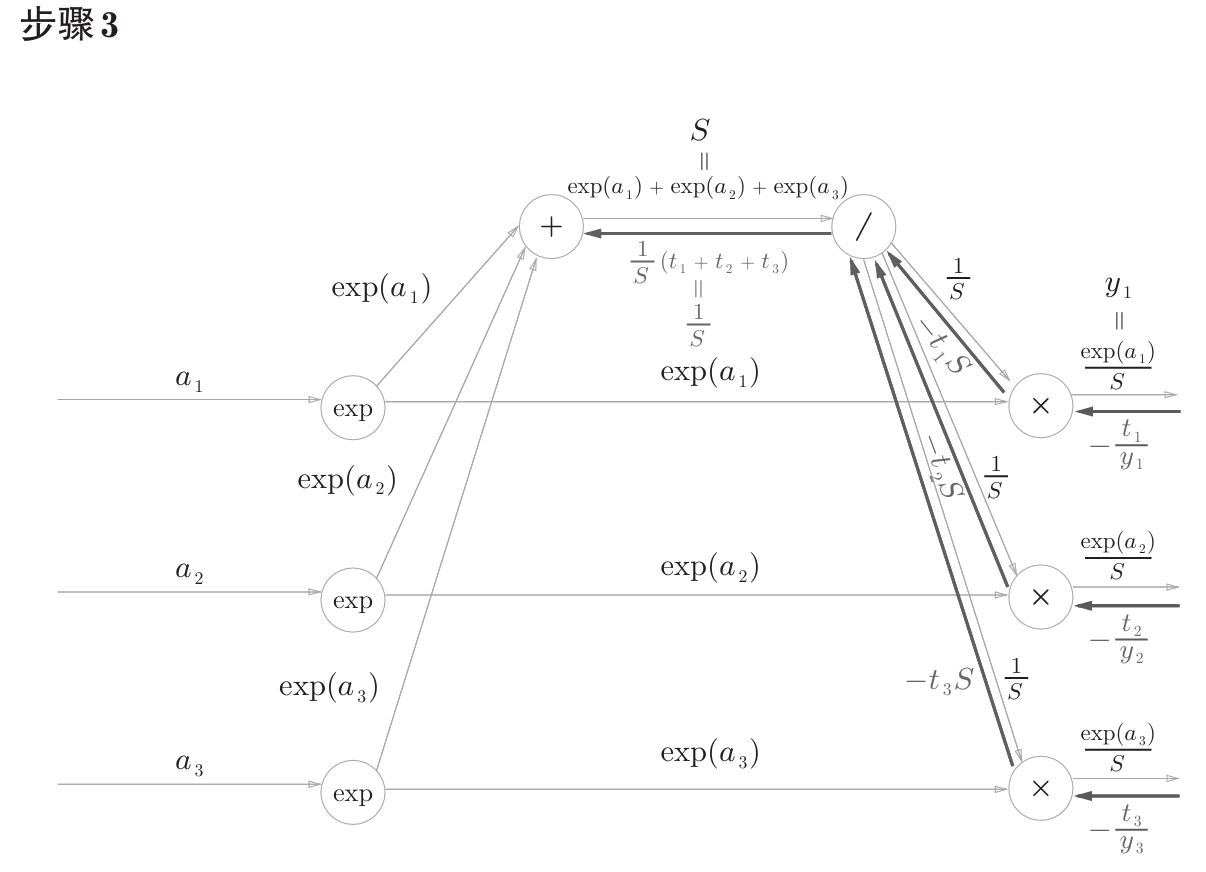
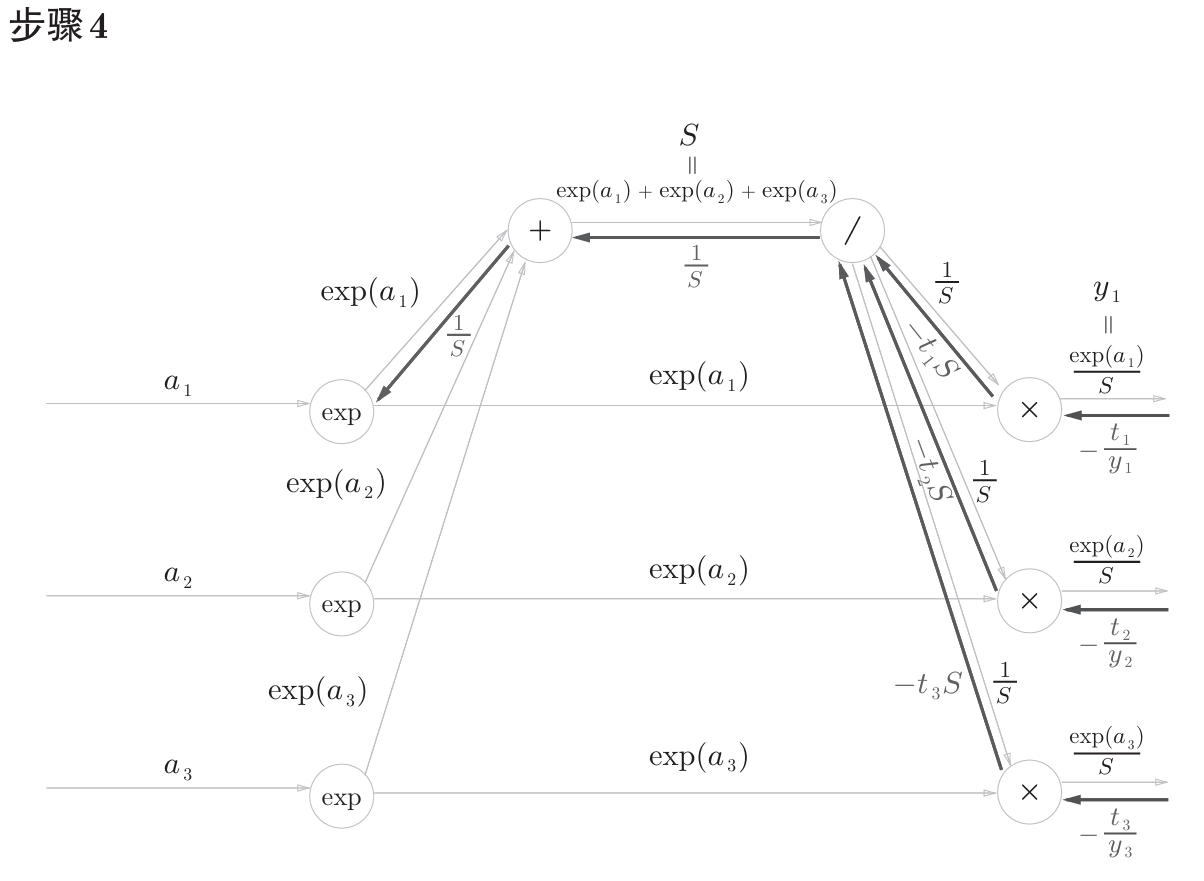
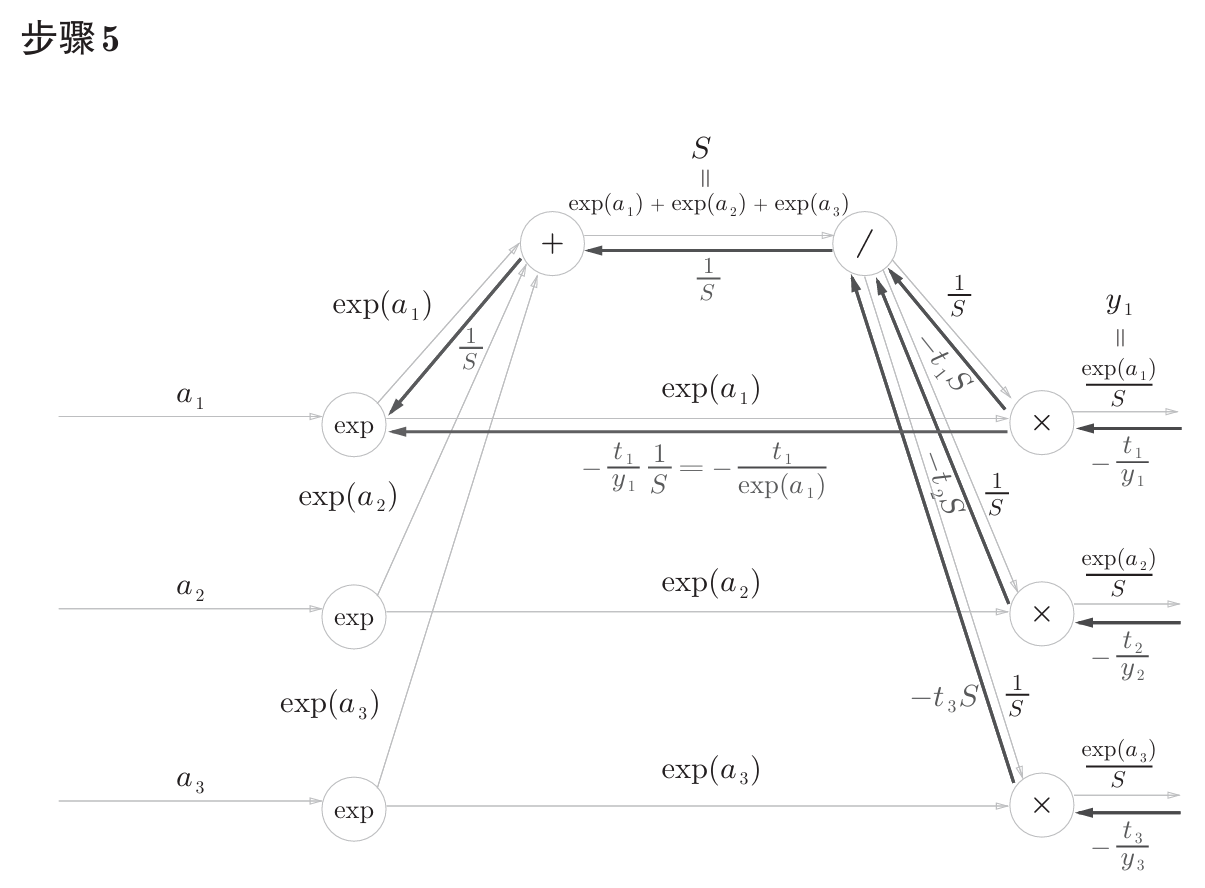
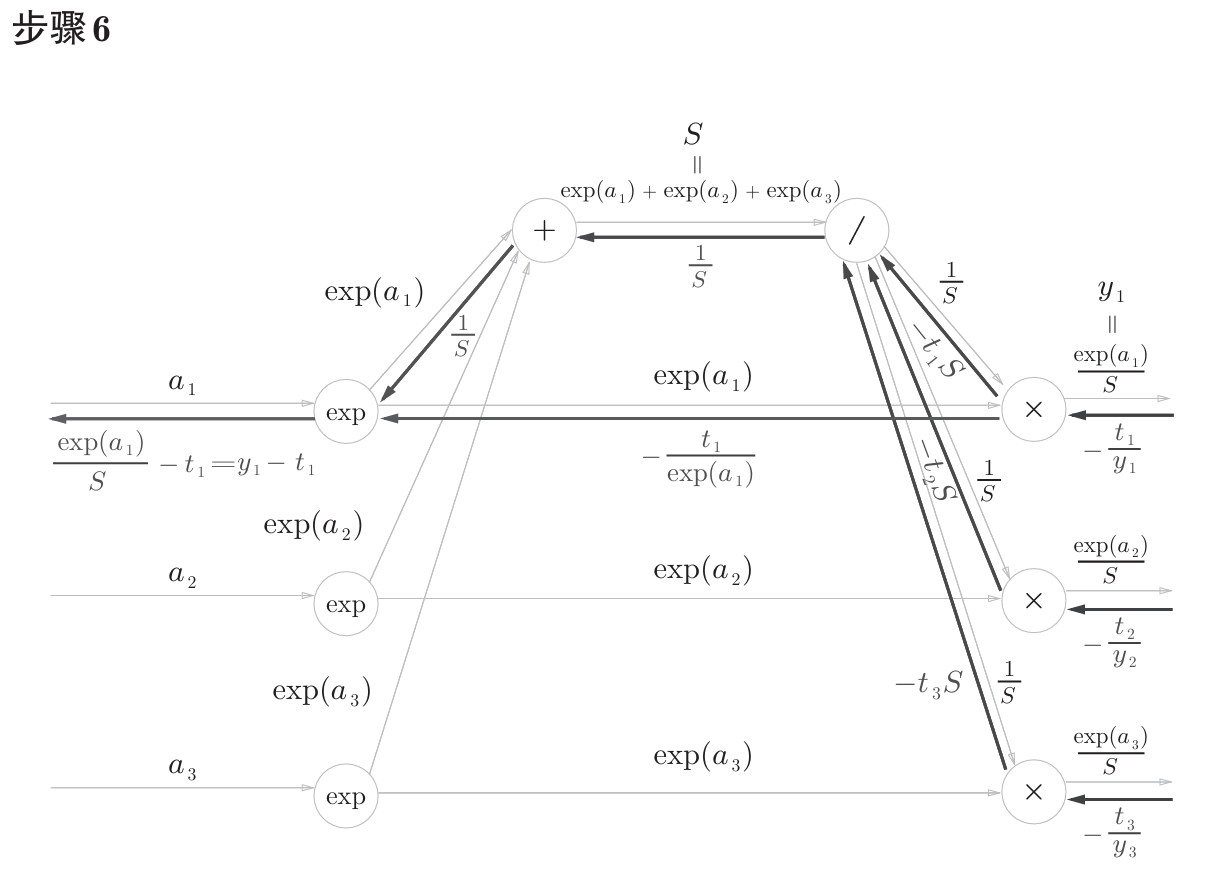
公式中的 $t_1$,$t_2$,$t_3$ 是监督数据(one-hot表示),最终简化的结果非常简洁 $(y_1-t_1,y_2-t_2,y_3-t_3)$ ,即 $y-t$ 。
代码实现如下。注意反向传播中除以批大小,得到整批样本的平均误差。因为 Layer 的 backward 设计是接收的 dout 是一个向量,所以这里除以 batch_size。
from common.functions import cross_entropy_error, softmax
class SoftmaxWithLossLayer:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self, x: np.ndarray, *, t: Optional[np.ndarray] = None):
self.y = softmax(x)
if t is not None:
self.t = t
self.loss = cross_entropy_error(self.y, self.t)
return self.y
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx
def optimize(self, lr):
pass
梯度确认
为了验证正确性,可以使用梯度确认方法。
梯度确认法是比较数值微分的结果和误差反向传播法结果,以确认误差反向传播法的实现是否正确。
数值微分法的结果和误差反向传播法结果的差值,如果很大,则说明反向传播法的实现有误。 因为数值微分法本身结果是存在误差的,所以只要差值非常小,就可以认为反向传播法的实现是正确的。 (对菜鸡而言,大佬应该一眼就看出来对不对了)
那么梯度接下来用梯度确认法验证上面的 ReLU、Sigmoid、Affine、SoftmaxWithLoss 的实现是否正确。
import unittest
from common import layers
from common.functions import relu, sigmoid
class TestReLU(unittest.TestCase):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.layer = ReLULayer()
def test_forward(self):
# 正向传播结果
x = np.array([[1, 2],
[3, 4]])
expected = np.array([[1, 2],
[3, 4]])
# 比较手算结果
self.assertTrue(np.array_equal(self.layer.forward(x), expected))
# 比较书附带源码的 relu 实现结果
self.assertTrue(np.array_equal(relu(x), self.layer.forward(x)))
def test_backward(self):
x = np.array([[1., 2.],
[3., 4.],
[-1., -1.]])
dout = np.array([[1., 1.],
[1., 1.],
[1., 1.]])
expected = np.array([[1., 1.],
[1., 1.],
[0., 0.]])
# 先做一次正向传播才能计算反向传播
self.layer.forward(x)
# 对比手算结果
self.assertTrue(np.array_equal(self.layer.backward(dout), expected))
# 对比数值微分法结果
d = 1.e-5
dx = (relu(x + d) - relu(x - d)) / (2 * d)
self.assertTrue(np.allclose(self.layer.backward(dout), dx))
class TestSigmoid(unittest.TestCase):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.layer = SigmoidLayer()
def test_forward(self):
x = np.array([[1., 2.],
[3., 4.]])
expected = np.array([[0.73105858, 0.88079708],
[0.95257413, 0.98201379]])
# 比较手算结果
self.assertTrue(np.allclose(self.layer.forward(x), expected))
# 比较书附带源码的 sigmoid 计算结果
self.assertTrue(np.allclose(self.layer.forward(x), sigmoid(x)))
def test_backward(self):
x = np.array([[1., 2.],
[3., 4.]])
dout = np.array([[1., 1.],
[1., 1.]])
expected = np.array([[0.19661193, 0.10499359],
[0.04517666, 0.01766271]])
self.layer.forward(x)
dx = self.layer.backward(dout)
# 比较手算结果
self.assertTrue(np.allclose(dx, expected))
# 比较数值微分法结果
d = 1.e-5
ndx = (sigmoid(x + d) - sigmoid(x - d)) / (2 * d)
self.assertTrue(np.allclose(dx, ndx))
class TestAffine(unittest.TestCase):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
# 2输入3神经元
self.layer = AffineLayer(np.array([[1., 1., 1.],
[1., 1., 1.]]),
np.array([0., 0., 0.]))
def test_forward(self):
x = np.array([[1., 2.],
[3., 4.]])
expected = np.array([[3., 3., 3.],
[7., 7., 7.]])
y = self.layer.forward(x)
self.assertTrue(np.allclose(y, expected))
def test_backward(self):
x = np.array([[1., 2.],
[3., 4.]])
dout = np.array([[1., 1., 1.],
[1., 1., 1.]])
y = self.layer.forward(x)
dx = self.layer.backward(dout)
# TODO: 如何数值微分法计算dx?
layer = layers.Affine(self.layer.w, self.layer.b)
layer.forward(x)
expected = layer.backward(dout)
# 验证
self.assertTrue(np.allclose(dx, expected))
class TestSoftmaxWithLoss(unittest.TestCase):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.layer = SoftmaxWithLossLayer()
def test_forward(self):
x = np.array([[1., 2., 3.],
[4., 5., 6.]])
t = np.array([[0., 0., 1.],
[0., 0., 1.]])
expected = 0.4076058141229194
self.layer.forward(x, t=t)
self.assertAlmostEqual(self.layer.loss, expected)
def test_backward(self):
x = np.array([[1., 4., 5.]])
t = np.array([[0., 0., 1.]])
dout = 1.
self.layer.forward(x, t=t)
dx = self.layer.backward(dout)
# TODO: 如何验证 softmax-with-loss 的反向传播结果?
layer = layers.SoftmaxWithLoss()
layer.forward(x, t)
expected = layer.backward()
# 验证
self.assertTrue(np.allclose(dx, expected))
_ = unittest.main(argv=[''], verbosity=2, exit=False)
test_backward (__main__.TestAffine) ... ok
test_forward (__main__.TestAffine) ... ok
test_backward (__main__.TestReLU) ... ok
test_forward (__main__.TestReLU) ... ok
test_backward (__main__.TestSigmoid) ... ok
test_forward (__main__.TestSigmoid) ... ok
test_backward (__main__.TestSoftmaxWithLoss) ... ok
test_forward (__main__.TestSoftmaxWithLoss) ... ok
----------------------------------------------------------------------
Ran 8 tests in 0.005s
OK
反向传播学习实例
不使用书中代码。模型还是采用3层神经网络,输入层、隐藏层、输出层。输入层神经元50个,隐藏层神经元100个,输出层神经元10个。输入信号 784 个。
from dataset.mnist import load_mnist
class SimpleNet:
def __init__(self):
self.layers = [
AffineLayer(np.random.randn(784, 50), np.random.randn(50)),
ReLULayer(),
AffineLayer(np.random.randn(50, 100), np.random.randn(100)),
ReLULayer(),
AffineLayer(np.random.randn(100, 10), np.random.randn(10)),
SoftmaxWithLossLayer(),
]
def predict(self, x, t=None):
y = x
for l in self.layers:
y = l.forward(y, t=t)
return y
def backward(self):
dout = 1
for l in reversed(self.layers):
dout = l.backward(dout)
def optimize(self, lr):
for l in self.layers:
l.optimize(lr)
def loss(self):
if hasattr(self.layers[-1], 'loss'):
return self.layers[-1].loss
return None
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
return np.sum(y == t) / float(x.shape[0])
def mini_batch(training_data, labels, batch_size):
""" 在数据集中随机抽取 mini-batch
"""
mask = np.random.choice(training_data.shape[0], batch_size)
return training_data[mask], labels[mask]
# 加载数据
(x_train, t_train), (x_test, t_test) = load_mnist(one_hot_label=True)
n = SimpleNet()
# 训练
for i in range(10000):
x, t = mini_batch(x_train, t_train, 100)
n.predict(x, t)
n.backward()
n.optimize(0.01)
if i % 1000 == 0:
x, t = mini_batch(x_test, t_test, 100)
print(f'第{i}次训练 损失 {n.loss()} 正确率 {n.accuracy(x, t)}')
# 训练后的正确率
x, t = mini_batch(x_test, t_test, 100)
print('验证正确率', n.accuracy(x, t))
第0次训练 损失 14.786135330514808 正确率 0.1
第1000次训练 损失 3.5467239155184798 正确率 0.83
第2000次训练 损失 2.286845867506459 正确率 0.77
第3000次训练 损失 1.2440765516672603 正确率 0.87
第4000次训练 损失 1.9765579805296412 正确率 0.75
第5000次训练 损失 0.8591504698224851 正确率 0.87
第6000次训练 损失 1.180173605455945 正确率 0.87
第7000次训练 损失 0.5386356986940977 正确率 0.84
第8000次训练 损失 0.7360734923263227 正确率 0.82
第9000次训练 损失 0.9423206740379103 正确率 0.82
验证正确率 0.83